Artificial Intelligence Theory : 비지도 학습(Unsupervised Learning)

비지도 학습(Unsupervised Learning)

비지도 학습이란 레이블(Label)을 포함시키지 않고 데이터에 의해 컴퓨터(알고리즘)이 스스로 학습하는 방법입니다.

레이블이 존재하지 않기 때문에 특정한 패턴이나 규칙을 지정하여 모델을 생성합니다.

지도 학습에서는 훈련 데이터(train data)와 레이블(Label)이 각각 X와 Y의 역할을 했다면, 비지도 학습은 데이터(Data)로만 결과를 유추합니다.

즉, X를 일련의 규칙(f(x))을 통해 숨겨진 패턴을 찾는 것을 목표로 합니다.

훈련 데이터 없이 데이터를 대상으로 수행하므로, 목푯값이 없어 지도 학습과 다르게 사전 학습을 필요로하지 않습니다.

그러므로, 지도 학습과는 다르게 레이블이 없기 때문에 결과에 대한 성능평가가 어렵습니다.

비지도 학습에는 크게 군집화(Clustering), 이상치 탐지(Outlier Detection, Anomaly Detection), 차원 축소(Dimensionality Reduction) 등이 있습니다.

군집화(Clustering)

군집화란 입력 데이터를 기준으로 비슷한 데이터끼리 몇 개의 군집(cluster)으로 나누는 알고리즘입니다.

입력 데이터들의 특성을 고려하여 데이터를 분류하고, 같은 그룹으로 분류된 데이터끼리는 서로 비슷한 성질(위치, 평균, 편차 등)을 갖습니다.

반대로 서로 다른 그룹으로 분류된 데이터는 서로 다른 성질을 갖습니다.

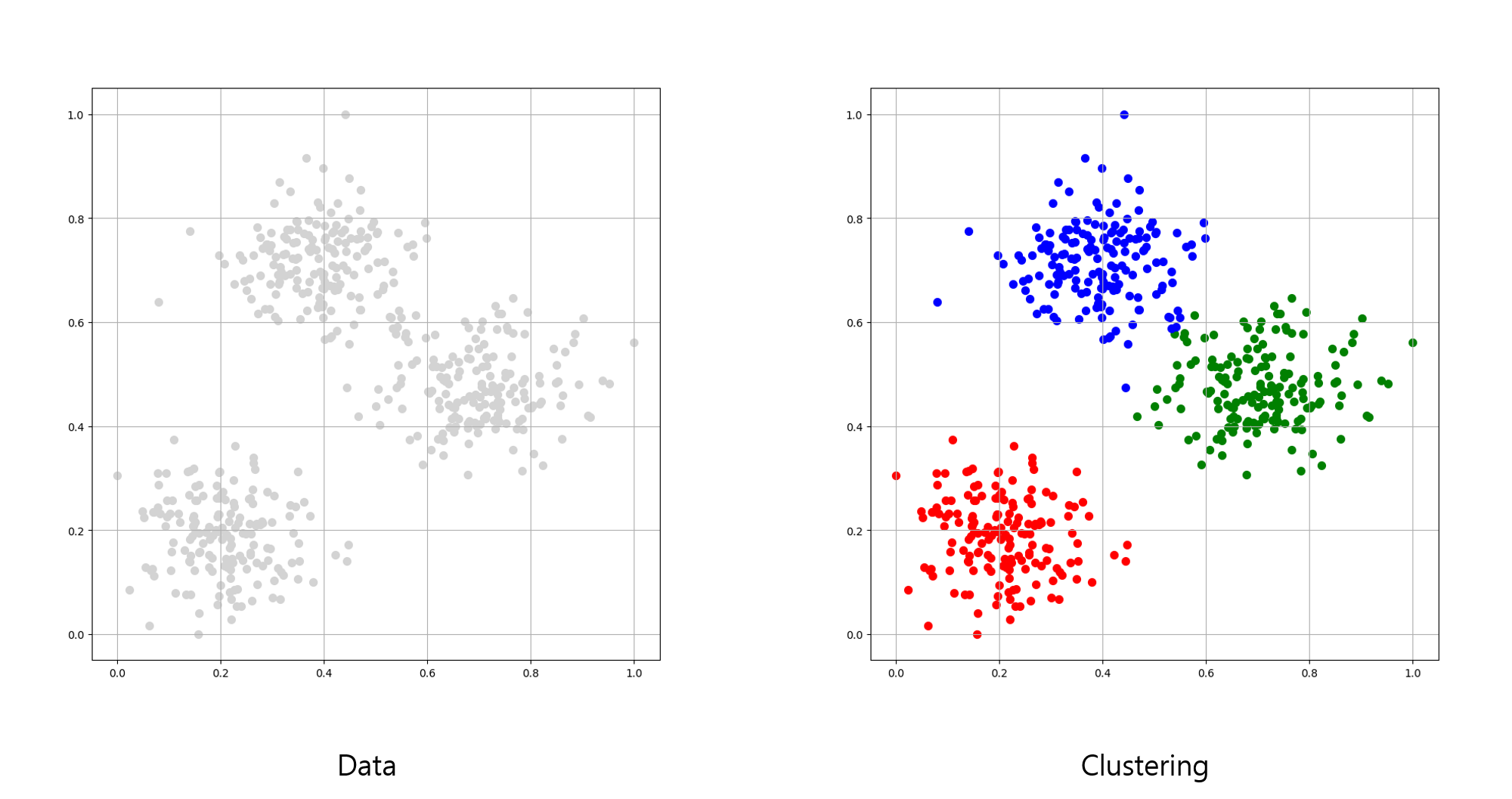
위 좌측 이미지는 제공된 데이터(Data)이며, 우측 이미지는 사전 학습 없이 일련의 규칙을 통해 분류한 결과입니다.

데이터의 비슷한 성질로 세 종류의 군집을 분류하였습니다.

군집화는 일반적인 정의가 존재하지 않기 때문에, 알고리즘마다 서로 다른 군집을 분류할 수 있습니다.

예를 들어, K-평균 군집화(K-Means Clustering)는 임의의 중심점(Centroid)을 기준으로 최소 거리에 기반한 군집화을 진행합니다.

각각의 데이터는 가장 가까운 중심에 군집을 이루며, 같은 중심에 할당된 데이터는 하나의 군집군으로 형성됩니다.

여기서 K는 군집의 갯수를 의미하며, k가 3일 때는 3개의 군집군을 형성합니다.

데이터들의 군집 중심에서 가장 가까운 군집으로 뭉쳐지게 됩니다.

K-평균 군집화는 중심의 초깃값이 무작위로 정해지며, K의 갯수만큼 군집을 이루게 됩니다.

중심점과 군집 개수로 나누기 때문에, 군집의 크기, 밀도, 형태가 특이하거나 서로 다를 경우 좋지 않은 결과가 나타날 수 있습니다.

밀도 기반 군집화(Density-based spatialclustering of applications with noise, DBSCAN)는 K-평균 군집화 방식과는 다르게 군집화를 진행합니다.

밀도 기반 군집화는 특정 공간 내에 데이터가 많이 몰려있는 부분을 대상으로 군집화 하는 알고리즘 입니다.

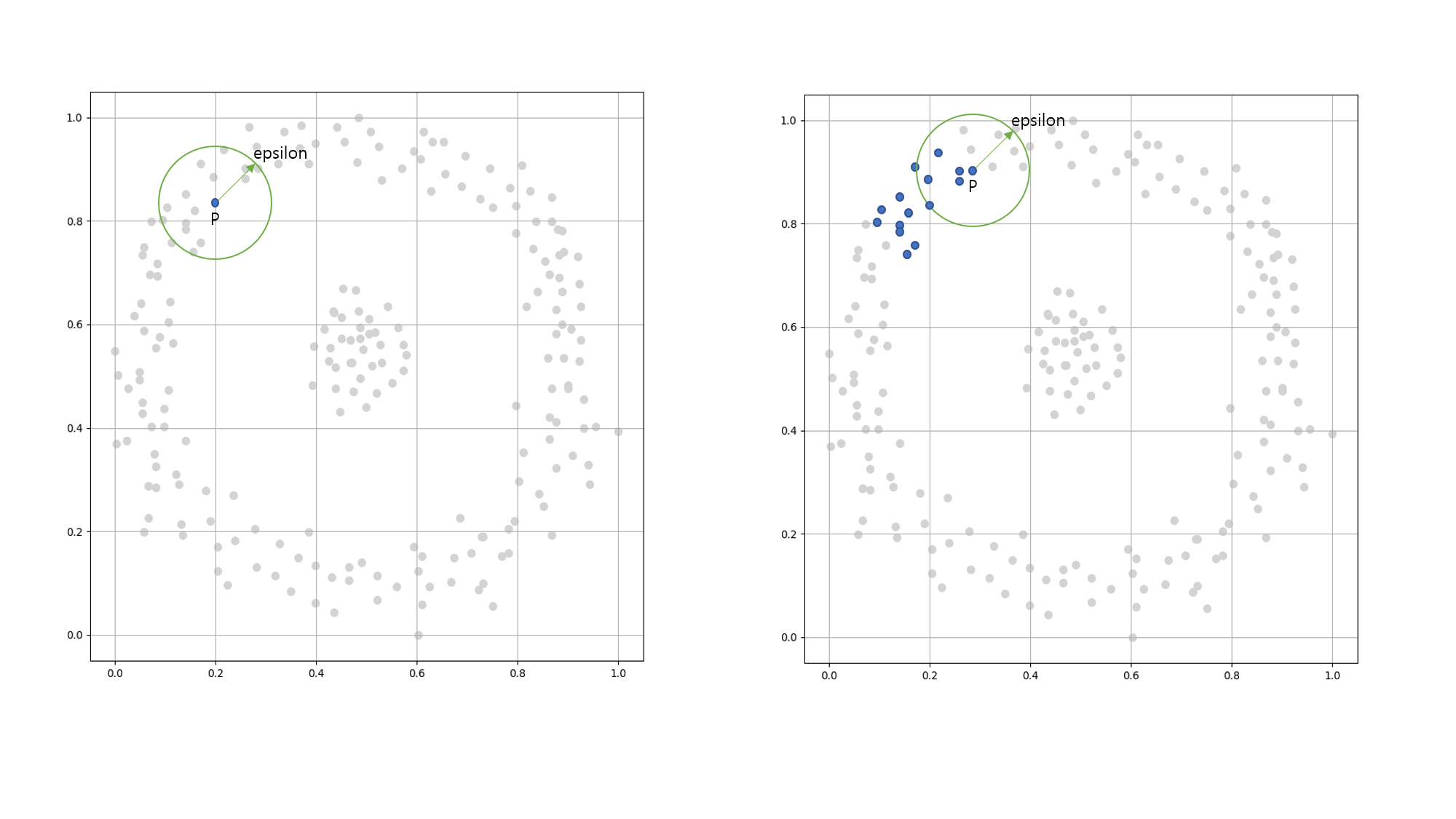
즉, 임의의 P점(sample)을 기준으로 특정 거리(epsilon) 내에 점이 M(MinSamples)개 이상 있다면 하나의 군집으로 간주합니다.

이 지역(특정 거리 안쪽)을 ε-이웃(epsilon-neighborhood)이라 부릅니다.

ε-이웃 안에 샘플이 M개 이상이라면, 핵심 샘플(core sample) 또는 핵심 지점(core point)이라 부르며, 이 과정을 반복합니다.

만약, 핵심 샘플이 아닌 영역은 이상치로 간주합니다.

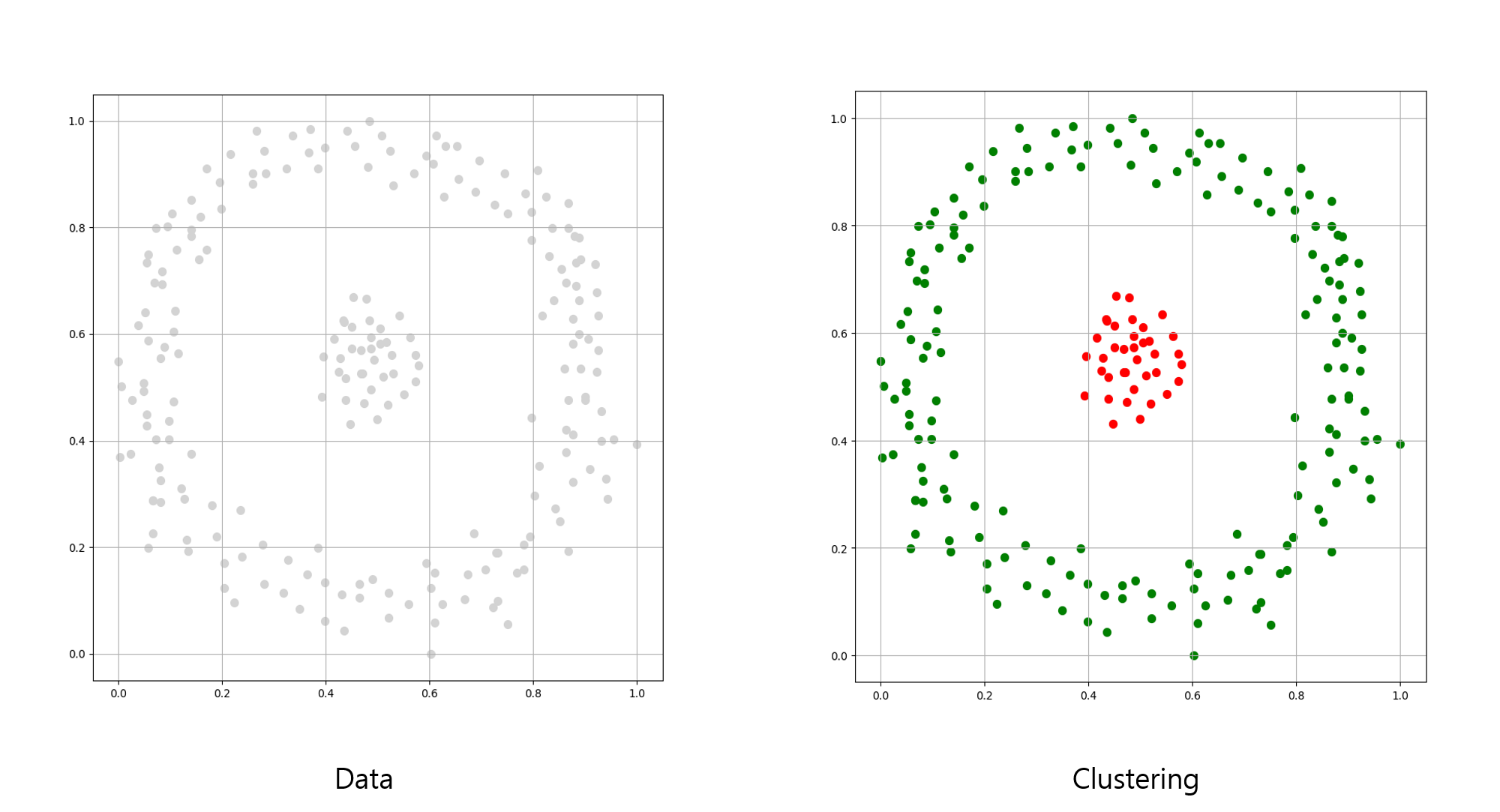
밀도 기반 군집화는 특정 거리와 최소 샘플 갯수로 군집화를 이루므로, 사전에 군집 갯수를 설정하지 않아도 됩니다.

또한, 밀도를 기준으로 군집화하기 때문에 복잡한 분포의 데이터를 분석할 수 있으며, 어떤 군집에도 속하지 않는 이상치를 구분할 수 있습니다.

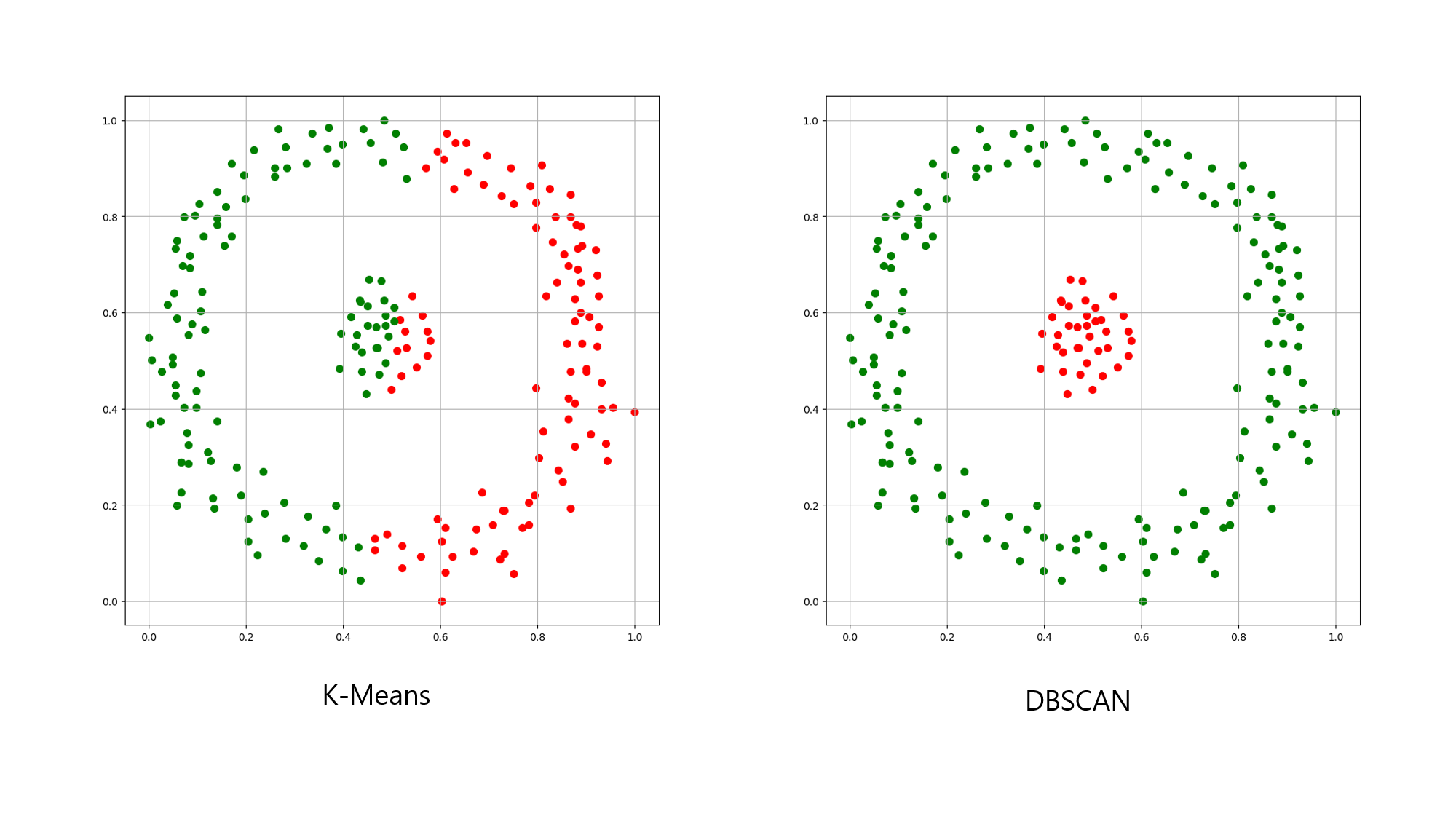
위 이미지는 같은 데이터를 K-평균 군집화와 밀도 기반 군집화로 군집화한 결과입니다.

군집화 알고리즘마다 군집화 하는 방식이 다르므로, 데이터의 특성과 수행할 알고리즘 또는 원하는 결과물에 따라 가장 효율적인 군집화 알고리즘을 선택해야 합니다.

군집화 알고리즘은 K-평균 군집화, 밀도 기반 군집화 이외에도 병합 군집화(Agglomerative Clustering), 평균 이동 군집화(Mean-Shift Clustering), 계층적 군집화(Hierarchical Clustering), 스펙트럼 군집화(Spectral Clustering) 등이 있습니다.

이상치 탐지(Outlier Dectection, Anomaly Detection)

이상치 탐지(Outlier Dectection, Anomaly Detection)는 어떤 군집에도 포함되지 않는 샘플을 의미합니다.

학습 데이터(train data)나 입력 데이터(input data)에 비정상적인 값을 갖는 데이터가 있다면, 이를 이상 데이터라 부릅니다.

정제되지 않은 빅데이터는 정상적인 데이터와 정상적이지 않은 데이터가 포함되어 있을 확률이 매우 높습니다.

정상적이지 않은 데이터를 이상 데이터로 간주합니다.

만약, 이상 데이터가 많다면 학습 모델이나 알고리즘에 정확도와 신뢰도를 낮추게 됩니다.

이상치 탐지는 결함이 있는 데이터나 제품을 찾거나, 시계열 데이터(Time Series data)에서 일반적인 패턴을 벗어난 패턴 등을 찾습니다.

이상치 탐지는 크게 이상치(Outlier)와 이상(Anomaly) 탐지가 있습니다.

이상치(Outlier)는 횡단면 데이터(Cross-sectional data)에서 비정상적인 데이터를 찾는 것을 의미합니다.

이상(Anomlay)는 시계열 데이터에서 비정상적인 데이터를 찾는 것을 의미합니다.

여기서, 일반적인 데이터는 정상치(Inlier)로 부르며 비정상적인 데이터는 이상치(Outlier)로 부릅니다.

• Tip : 시계열 데이터란 일정 시간을 간격으로 배치된 데이터를 의미합니다.

• Tip : 횡단면 데이터란 동일한 시간, 동일 기간에 여러 변수에 대하여 수집된 데이터를 의미합니다.

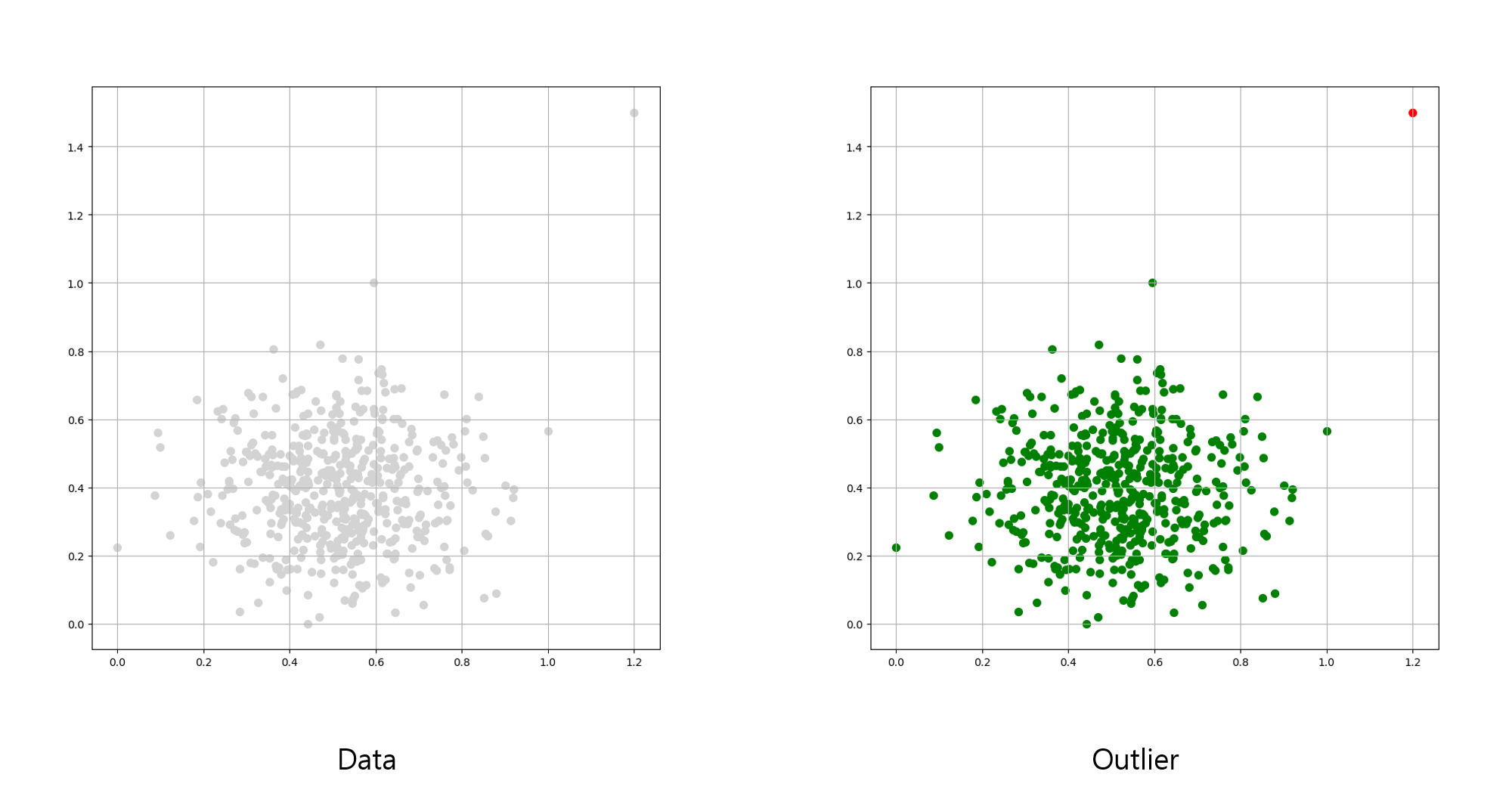
이상치는 위의 이미지에서 붉은색 지점이 이상치로 볼 수 있습니다.

주요한 군집에 포함되지 않으며, 갑자기 데이터가 크게 달라지는 부분을 확인할 수 있습니다.

이런 부분은 특정 알고리즘을 진행하기 전에, 사전에 제거하거나 별도의 분류를 진행해야 합니다.

만약, 이상치를 제거하지 않고 군집화 등을 진행한다면 의도하지 않은 결과가 나타날 수 있습니다.

이상치 탐지 알고리즘은 아이솔레이션 포레스트(Isolation Forest), LOF(Local Outlier Factors), One-class SVM 등이 있습니다.

차원 축소(Dimensionality Reduction)

차원 축소란 다차원의 데이터의 차원을 축소하여 저차원의 새로운 데이터로 변경해 생성하는 것을 의미합니다.

여러 특성과 변수 간에 존재하는 상관관계를 이용하여 주요 구성요소에 대한 분석을 진행합니다.

데이터에 특성(feature)이 매우 많다면 학습 모델을 구성하는 데 오랜 시간이 소요되며, 정확도와 신뢰도를 보장할 수 없습니다.

다차원의 데이터의 특성간에 상관관계가 서로 높다면, 하나의 특성만을 사용하거나 여러 특성을 조합하여 하나의 특성으로 변경할 수 있습니다.

만약, 3차원의 데이터를 2차원으로 축소한다고 가정하면 연산량의 감소, 노이즈 및 이상치 제거, 시각화 등에 이점을 볼 수 있습니다.

차원 축소에는 크게 특성 선택(Feature Selection)과 특성 추출(Feature Extraction)`이 있습니다.

특성 선택과 특성 추출은 앞서 설명한 변경법을 의미합니다.

특성 선택은 특정 특성에 종속적인 성향이 강해, 사용하지 않아도 되는 특성을 의미합니다.

예를 들어, 점수(score)와 등급(rank)에 관한 특성이 있다면 등급은 점수에 종속적인 데이터일 가능성이 높습니다.

그렇다면, 둘 중 하나의 특성을 제거하여 차원을 축소할 수 있습니다.

특성 추출은 점수와 등급에 관한 특성을 하나로 압축하여 새로운 특성을 만들어 내는 것 입니다.

예를 들어, 점수와 등급을 다시 산정해 기존 A, B, C 분류 방식에서 A+, A, B+, B, C+, C 등으로 새로운 특성을 만들어낼 수 있습니다.

차원 축소 알고리즘은 주성분 분석(Principal Component Analysis, PCA), 특잇값 분해(Singular Value Decomposition, SVD), 음수 미포함 행렬 분해(Non-negative Matrix Factorization, NMF) 등이 있습니다.

• Writer by : 윤대희