상위 목록: 하위 목록: 작성 날짜: 읽는 데 51 분 소요

순전파(Forward Propagation)

순전파(Forward Propagation)란 입력 데이터를 기반으로 신경망을 따라 입력층(Input Layer)부터 출력층(Output Layer)까지 차례대로 변수들을 계산하고 추론(Inference)한 결과를 의미합니다.

모델(Model)에 입력값(\(x\))을 입력하여 순전파(Forward) 연산을 진행합니다.

이 과정에서 계층(Layer)마다 가중치(Weight)와 편향(Bias)으로 계산된 값이 활성화 함수(Activation Function)에 전달됩니다.

최종 활성화 함수에서 출력값(\(\hat{y}\))이 계산되고 이 값을 손실 함수(Loss Function)에 실젯값(\(y\))과 함께 연산하여 오차(Cost)를 계산합니다.

자세한 과정은 순전파(Forward Propagation) 풀이에서 확인해볼 수 있습니다.



역전파(Back Propagation)

역전파(Back Propagation)란 순전파(Forward Propagation)의 방향과 반대로 연산이 진행됩니다.

순전파(Forward Propagation) 과정을 통해 나온 오차(Cost)를 활용해 각 계층(Layer)의 가중치(Weight)와 편향(Bias)을 최적화합니다.

역전파 과정에서는 각각의 가중치와 편향을 최적화 하기 위해 연쇄 법칙(Chain Rule)을 활용합니다.

새로 계산된 가중치는 최적화(Optimization) 알고리즘을 통해 실젯값과 예측값의 차이를 계산하여 오차를 최소로 줄일 수 있는 가중치(Weight)와 편향(Bias)을 계산하게 됩니다.

자세한 과정은 역전파(Back Propagation) 풀이에서 확인해볼 수 있습니다.



계산 방법(Method of calculation)

class CustomModel(nn.Module):
    def __init__(self):
        super(CustomModel, self).__init__()

        self.layer1 = nn.Sequential(
            nn.Linear(2, 2),
            nn.Sigmoid()
        )
        self.layer2 = nn.Sequential(
            nn.Linear(2, 1),
            nn.Sigmoid()
        )
        
        self.layer1[0].weight.data = torch.nn.Parameter(
            torch.Tensor([[0.4352, 0.3545],
                         [0.1951, 0.4835]])
        )

        self.layer1[0].bias.data = torch.nn.Parameter(
            torch.Tensor([-0.1419,  0.0439])
        )

        self.layer2[0].weight.data = torch.nn.Parameter(
            torch.Tensor([[-0.1725,  0.1129]])
        )

        self.layer2[0].bias.data = torch.nn.Parameter(
            torch.Tensor([-0.3043])
        )

임의의 인공 신경망(Neural Network)을 구성해 순전파(Forward Propagation)와 역전파(Back Propagation) 과정을 풀어보도록 하겠습니다.

풀이에 사용된 PyTorch 모델 구조 및 초깃값은 위와 같습니다.


criterion = nn.BCELoss().to(device)
optimizer = optim.SGD(model.parameters(), lr=1)

풀이에 사용되는 손실 함수(Loss Function)는 이진 교차 엔트로피(Binary Cross Entropy Loss)입니다.

최적화 함수(Optimization Function)는 확률적 경사 하강법(Stochastic Gradient Descent)입니다.

학습률(learning_rate)은 1로 설정하여 갱신되는 가중치를 확인하기 쉽게 할당합니다.

이진 교차 엔트로피(Binary Cross Entropy Loss)에 대한 자세한 내용은 제 12강 - 이진 분류(Binary Classification)에서 확인해볼 수 있습니다.

최적화 함수(Optimization Function)에 대한 자세한 내용은 제 5강 - 최적화(Optimization)에서 확인해볼 수 있습니다.


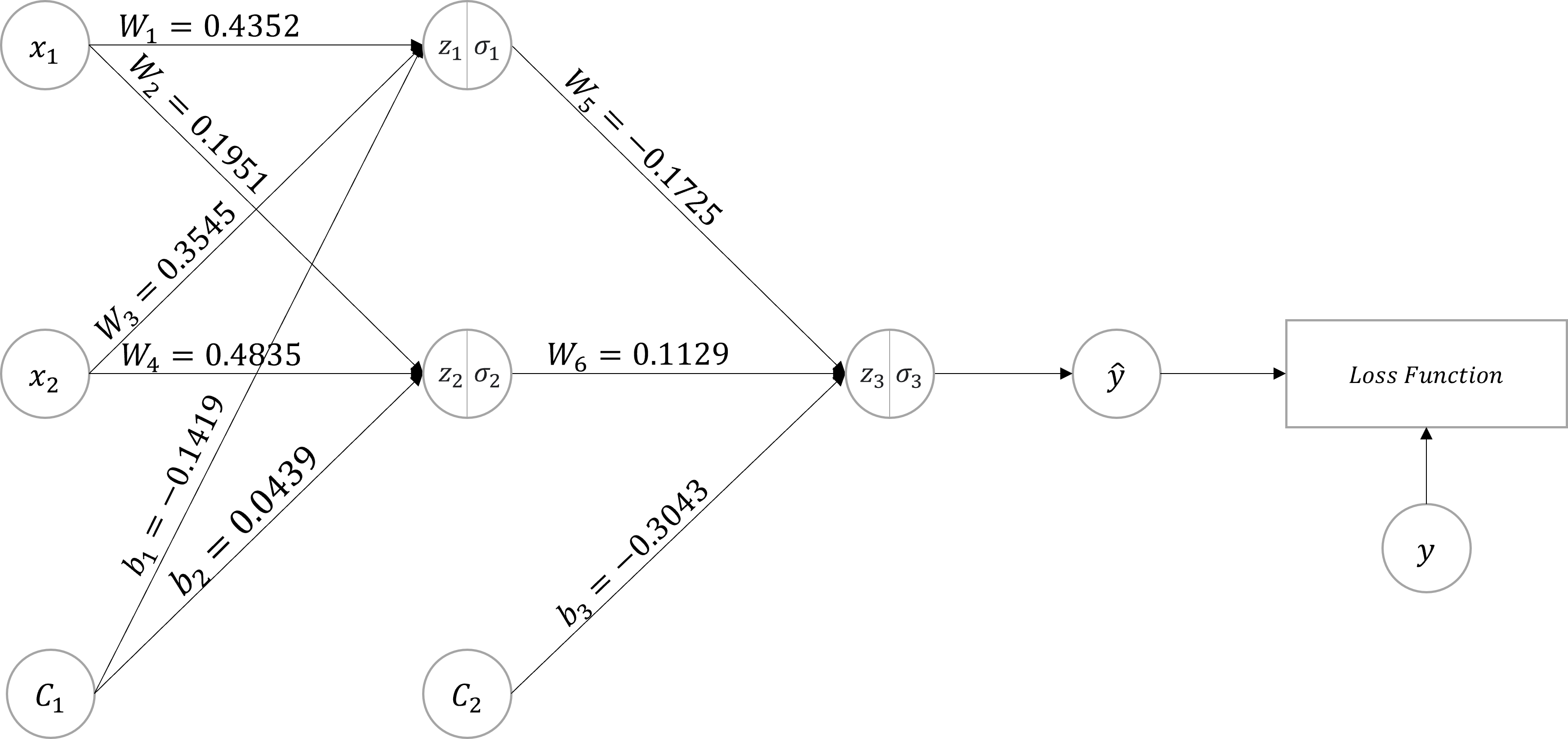
예제의 코드를 다이어그램으로 시각화 한다면 위 그림과 같이 표현할 수 있습니다.

입력값(x)과 실젯값(y)에 각각 [1, 1]과 [0]이 입력되었다고 가정합니다.

\[\begin{multline} \shoveleft \therefore x_1 = 1, \ x_2 = 1, \ y = 0 \end{multline}\] \[\begin{multline} \shoveleft \therefore C_1 = 1, \ C_2 = 1 \end{multline}\]
  • Tip : 상수(C)는 수식에서 생략합니다.
  • Tip : 풀이에서는 소수점 4자리까지만 표시합니다.


순전파(Forward Propagation) 풀이

첫 번째 계층의 가중합(Weighted Sum)을 계산합니다.

\(z\)는 가중합으로서, 입력값(\(x\))와 가중치(\(W\))의 곱을 모두 더한 값에 편향(\(b\))을 더한 값을 의미합니다.

$$ \begin{aligned} z_1 & =W_{1}x_{1} + W_{2}x_{2} + b_{1}\\ & =0.4352\times1 + 0.3545\times1 - 0.1419\\ & =0.6478 \end{aligned} $$
$$ \begin{align} z_2 & =W_{3}x_{1} + W_{4}x_{2} + b_{2}\\ & =0.1951\times1 + 0.4835\times1 + 0.0439\\ & =0.7225 \end{align} $$


가중합(Weighted Sum)이 완료됐다면, 활성화 함수(Activation Function)를 적용합니다.

현재 예제에서는 시그모이드(Sigmoid)가 적용되었습니다.

$$ \begin{align} \sigma_1 & =\frac{1}{1+e^{-z_1}}\\ & =\frac{1}{1+e^{-0.6478}}\\ & =0.6565 \end{align} $$
$$ \begin{align} \sigma_2 & =\frac{1}{1+e^{-z_2}}\\ & =\frac{1}{1+e^{-0.7225}}\\ & =0.6732 \end{align} $$


\(\sigma\)를 계산했다면, 이 값을 입력값으로 사용하여 동일한 방식으로 가중합(Weighted Sum)과 시그모이드(Sigmoid)가 적용된 값을 계산합니다.

$$ \begin{align} z_3 & =W_{5}\sigma_{1} + W_{6}\sigma_{2} + b_{3}\\ & =-0.1725\times0.6565 + 0.1129\times0.6731 - 0.3043\\ & =-0.3415 \end{align} $$
$$ \begin{align} \sigma_3 & =\frac{1}{1+e^{-z_3}}\\ & =\frac{1}{1+e^{0.3415}}\\ & =0.4154 \end{align} $$

PyTorch 코드에서는 output = model(x)이 순전파 과정입니다.

\(\sigma_3\)이 output 변수에 할당됩니다.


오차(Cost) 계산

최종으로 계산된 \(\sigma_3\)는 예측값(\(\hat{y}\))이 됩니다.

이 예측값을 활용하여 오차(Cost)를 계산합니다.

$$ \begin{align} \mathcal{L} & = -( y log (\hat{y}) + (1 - y) log (1 - \hat{y})) \\ & =-( 0 log (0.4154) + (1 - 0) log (1 - 0.4154)) \\ &= -log0.5846 \\ &=0.5368 \end{align} $$

PyTorch 코드에서는 loss = criterion(output, y)이 오차 계산 과정입니다.

\(\mathcal{L}\)이 loss 변수에 할당됩니다.


역전파(Back Propagation) 풀이

역전파(Back Propagation) 과정에서는 계층(Layer)의 역순으로 가중치(Weight)와 편향(Bias)을 갱신(Update)합니다.

즉, \(W_5, W_6, b_3\)를 갱신한 다음에 \(W_1, W_2, W_3, W_4, b_1, b_2\)가 갱신됩니다.

모델의 학습은 오차가 작아지는 방향으로 갱신되어야 하기 때문에 미분값이 0에 가까워져야 합니다.

그러므로, 갱신된 가중치와 편향의 기울기는 오차가 0이 되는 방향으로 진행하게 됩니다.

갱신된 가중치나 편향은 위에서 계산된 기울기를 감산해, 변화가 없을 때 까지 반복하게 됩니다.

이를 수식으로 표현한다면 다음과 같습니다.

\[\begin{multline} \shoveleft \therefore W_n(t+1) = W_n(t) - \alpha\frac{\partial\mathcal{L}}{\partial W_n(t)} \end{multline}\]


지속적으로 가중치를 갱신하게 되면, \(\frac{\partial\mathcal{L}}{\partial W_n(t)}\)는 점점 0에 가까워지게 됩니다.

이는 오차가 0에 가까워 지도록 가중치가 갱신되며, \(W_n(t+1) = W_n(t)\)가 되어 학습이 완료됩니다.

즉, 순전파를 통해 오차를 계산하고 역전파 과정을 통해 오찻값이 0이 될 수 있도록 가중치를 갱신합니다.

위와 같은 일련의 과정을 계속 반복합니다. 먼저, \(W_5\)의 가중치를 갱신해보도록 하겠습니다.

  • Tip : \(t\)는 가중치 갱신 횟수를 의미합니다.
  • Tip : \(\alpha\)는 학습률(Learning Rate)을 의미합니다. 예제에서는 1로 할당하였습니다.


$$ \begin{align} W_5(2) & = W_5(1) - \alpha\frac{\partial\mathcal{L}}{\partial W_5(1)} \\ & = -0.1725 - \frac{\partial\mathcal{L}}{\partial W_5(1)} \end{align} $$

\(W_5(2)\) 를 계산하기 위해서는 오차를 가중치로 편미분한 값을 계산해야 합니다.

연쇄 법칙(Chain Rule)을 적용해 미분을 진행합니다. \(W_5(1)\)는 편의상 \(W_5\)로 표기하도록 하겠습니다.


$$ \begin{align} \frac{\partial\mathcal{L}}{\partial W_5} & =\frac{\partial\mathcal{L}}{\partial \sigma_3} \times \frac{\partial \sigma_3}{\partial z_3} \times \frac{\partial z_3}{\partial W_5} \end{align} $$

연쇄 법칙(Chain Rule)을 통해 세 개의 항이 생성되며, 각각 편미분을 진행합니다.

각 항의 포함된 변수 및 수식은 순전파(Forward Propagation) 풀이에서 확인해볼 수 있습니다.


$$ \begin{align} \frac{\partial\mathcal{L}}{\partial \sigma_3} & = -\frac{\partial}{\partial \sigma_3}( y log (\hat{y}) + (1 - y) log (1 - \hat{y})) \\ & =-\frac{\partial}{\partial \sigma_3}( y log (\sigma_3) + (1 - y) log (1 - \sigma_3)) \\ & =-(\frac{y}{\sigma_3} - \frac{1-y}{1-\sigma_3}) \\ & = \frac{\sigma_3 - y}{\sigma_3 (1 - \sigma_3)} \\ & = \frac{\sigma_3}{\sigma_3 (1 - \sigma_3)} \\ & = \frac{0.4154}{0.4154(1-0.4154)} \\ & = 1.7106 \end{align} $$


$$ \begin{align} \frac{\partial \sigma_3}{\partial z_3} & = \frac{\partial}{\partial z_3} (\frac{1}{1+e^{-z_3}}) \\ & = \frac{e^{-z_3}}{(1+e^{-z_3})^2} \\ & = \frac{1}{1+e^{-z_3}} \times (1 - \frac{1}{1+e^{-z_3}}) \\ & = \sigma_3 \times (1 - \sigma_3) \\ & = 0.2428 \end{align} $$


$$ \begin{align} \frac{\partial z_3}{\partial W_5} & = \frac{\partial}{\partial W_5} (W_{5}\sigma_{1} + W_{6}\sigma_{2} + b_{3}) \\ & = \sigma_{1} \\ & = 0.6565 \end{align} $$


$$ \begin{align} \frac{\partial\mathcal{L}}{\partial W_5} & =\frac{\partial\mathcal{L}}{\partial \sigma_3} \times \frac{\partial \sigma_3}{\partial z_3} \times \frac{\partial z_3}{\partial W_5} \\ & = 1.7106 \times 0.2428 \times 0.6565 \\ & = 0.2727\end{align} $$


$$ \begin{align} W_5(2) & = W_5(1) - \alpha\frac{\partial\mathcal{L}}{\partial W_5(1)} \\ & = -0.1725 - \frac{\partial\mathcal{L}}{\partial W_5(1)} \\ & = -0.1725 - \frac{\partial\mathcal{L}}{\partial W_5} \\ & = -0.1725 - 0.2727 \\ & = -0.4452 \end{align} $$

위와 같은 과정을 통해 \(W_5\)의 가중치를 갱신합니다.

동일한 방식으로 \(W_6\) 과 \(b_3\)도 갱신합니다.


$$ \begin{align} W_6(2) & = W_6(1) - \alpha\frac{\partial\mathcal{L}}{\partial W_6(1)} \\ & = W_6(1) -\frac{\partial\mathcal{L}}{\partial \sigma_3} \times \frac{\partial \sigma_3}{\partial z_3} \times \frac{\partial z_3}{\partial W_6} \\ & = 0.1129 - 1.7106 \times 0.2428 \times 0.6732 \\ & = -0.1667\end{align} $$


$$ \begin{align} b_3(2) & = b_3(1) - \alpha\frac{\partial\mathcal{L}}{\partial b_3(1)} \\ & = b_3(1) -\frac{\partial\mathcal{L}}{\partial \sigma_3} \times \frac{\partial \sigma_3}{\partial z_3} \times \frac{\partial z_3}{\partial b_3} \\ & = -0.3043 - 1.7106 \times 0.2428 \times 1.0000 \\ & = -0.7196\end{align} $$

이로써 \(W_5, W_6, b_3\)의 가중치와 편향이 갱신됐습니다.

다음으로 갱신해야하는 \(W_1, W_2, W_3, W_4, b_1, b_2\)도 동일한 방식으로 갱신합니다.

먼저, \(W_1\)의 가중치를 갱신해보도록 하겠습니다.


$$ \begin{align} W_1(2) & = W_1(1) - \alpha\frac{\partial\mathcal{L}}{\partial W_1(1)} \\ & = W_1(1) -\frac{\partial\mathcal{L}}{\partial \sigma_1} \times \frac{\partial \sigma_1}{\partial z_1} \times \frac{\partial z_1}{\partial W_1} \\ & = 0.4352 - \frac{\partial\mathcal{L}}{\partial W_1(1)} \times 0.2255 \times 1.0000\end{align} $$

위 수식과 같이 동일한 방식으로 \(W_1\) 가중치를 갱신하려고 한다면, 오차 함수를 미분하려는 과정에서 복잡한 수식으로 변경될 수 있습니다.

그러므로, 이 부분도 연쇄 법칙(Chain Rule)을 적용해 미분을 진행합니다.


$$ \begin{align} \frac{\partial\mathcal{L}}{\partial W_1(1)} & = \frac{\partial\mathcal{L}}{\partial \sigma_3} \times \frac{\partial \sigma_3}{\partial z_3} \times \frac{\partial z_3}{\partial \sigma_1} \\ & = 1.7106 \times 0.2428 \times W_5 \\ & = -0.0717\end{align} $$

연쇄 법칙(Chain Rule)을 적용한다면 복잡한 연산을 진행하지 않아도 편미분값을 확인할 수 있습니다.

이 값을 활용해 \(W_1(2)\)의 결괏값을 확인합니다.


$$ \begin{align} W_1(2) & = 0.4352 - \frac{\partial\mathcal{L}}{\partial W_1(1)} \times 0.2428 \times 1.0000 \\ & = 0.4352 + 0.0717 \times 0.2255 \times 1.0000 \\ & = 0.4514\end{align} $$

\(W_1(2)\)는 \(0.4352\)에서 \(0.4514\)로 갱신된 것을 확인할 수 있습니다.

나머지 \(W_2, W_3, W_4, b_1, b_2\)도 동일한 방식으로 갱신합니다.


$$ \begin{align} W_2(2) & = W_2(1) - \alpha\frac{\partial\mathcal{L}}{\partial W_2(1)} \\ & = W_2(1) -\frac{\partial\mathcal{L}}{\partial \sigma_2} \times \frac{\partial \sigma_2}{\partial z_2} \times \frac{\partial z_2}{\partial W_2} \\ & = 0.1848\end{align} $$


$$ \begin{align} W_3(2) & = W_3(1) - \alpha\frac{\partial\mathcal{L}}{\partial W_3(1)} \\ & = W_3(1) -\frac{\partial\mathcal{L}}{\partial \sigma_1} \times \frac{\partial \sigma_1}{\partial z_1} \times \frac{\partial z_1}{\partial W_3} \\ & = 0.3707\end{align} $$


$$ \begin{align} W_4(2) & = W_4(1) - \alpha\frac{\partial\mathcal{L}}{\partial W_4(1)} \\ & = W_4(1) -\frac{\partial\mathcal{L}}{\partial \sigma_2} \times \frac{\partial \sigma_2}{\partial z_2} \times \frac{\partial z_2}{\partial W_4} \\ & = 0.4732\end{align} $$


$$ \begin{align} b_1(2) & = b_1(1) - \alpha\frac{\partial\mathcal{L}}{\partial b_1(1)} \\ & = b_1(1) -\frac{\partial\mathcal{L}}{\partial \sigma_1} \times \frac{\partial \sigma_1}{\partial z_1} \times \frac{\partial z_1}{\partial b_1} \\ & = -0.1257\end{align} $$


$$ \begin{align} b_2(2) & = b_2(1) - \alpha\frac{\partial\mathcal{L}}{\partial b_2(1)} \\ & = b_2(1) -\frac{\partial\mathcal{L}}{\partial \sigma_2} \times \frac{\partial \sigma_2}{\partial z_2} \times \frac{\partial z_2}{\partial b_2} \\ & = 0.0336\end{align} $$

모든 가중치와 편향을 갱신하면 학습이 1회 진행되었다고 볼 수 있습니다.

갱신된 가중치와 편향으로 다음 번 학습을 진행하며, 오차(Cost)가 점차 감소하게 됩니다.

현재 예제에서는 배치 크기(Batch Size)를 1로 가정하고 풀이했습니다.

만약, 배치 크기가 1보다 크다면 행렬로 풀이를 진행합니다.


가중치와 편향 갱신 비교

\[\begin{align} \textbf{Layer #1}\\ W_1(1) & =0.4352 & W_1(2) & =0.4514 \\ W_2(1) & =0.1951 & W_2(2) & =0.1848 \\ W_3(1) & =0.3545 & W_3(2) & =0.3707 \\ W_4(1) & =0.4835 & W_4(2) & =0.4732 \\ b_1(1) & =-0.1419 & b_1(2) & =-0.1257 \\ b_2(1) & =0.0439 & b_2(2) & =0.0336 \\\\ \textbf{Layer #2}\\ W_5(1) & =-0.1725 & W_5(2) & =-0.4452 \\ W_6(1) & =0.1129 & W_6(2) & =-0.1667 \\ b_3(1) & =-0.3043 & b_3(2) & =-0.7196 \end{align}\]

계층(Layer)별로 갱신값을 비교해본다면 위와 같이 정리할 수 있습니다.

학습률(learning_rate)을 비교적 큰 1로 주었음에도 불구하고, Layer #1의 변화량은 Layer #2와 비교했을 때 크지 않습니다.

현재 모델에서 사용한 활성화 함수(Activation Function)는 시그모이드(Sigmoid)를 적용하였습니다.

시그모이드(Sigmoid)는 출력값의 범위를 0 ~ 1 사이로 제한하기 때문에 역전파(Back Propagation) 과정에서 0에 가까운 기울기가 곱해지게 됩니다.

그러므로, 역전파 과정에서 입력층의 방향으로 값을 전달하는 과정에서 0에 수렴되는 문제가 발생해 성능이 떨어지게 됩니다.

출력층(Output Layer)에 가까운 Layer #2는 변화량이 높게되고, 입력층(Input Layer)에 가까운 Layer #1은 변화량이 미미해집니다.

이러한 이유로 깊은(Deep) 모델의 은닉층(Hidden Layer)에서는 시그모이드(Sigmoid)를 활성화 함수로 사용하지 않습니다.

시그모이드(Sigmoid)에 대한 자세한 내용은 제 12강 - 이진 분류(Binary Classification)에서 확인해볼 수 있습니다.



  • Writer by : 윤대희

댓글 남기기

최근 포스트