Python Pytorch 강좌 : 제 13강 - 다중 분류(Multiclass Classification)

상위 목록: Python 하위 목록: PyTorch 작성 날짜: 2022-04-09 읽는 데 53 분 소요

다중 분류(Multiclass Classification)

다중 분류(Multiclass Classification)란 규칙에 따라 입력된 값을 세 그룹 이상으로 분류하는 작업을 의미합니다.

구분하려는 결과가 A 그룹, B 그룹, C 그룹 등으로 데이터를 나누는 경우를 의미합니다.

하나의 특성(feature)이나 여러 개의 특성(feature)으로부터 나온 값을 계산해 각각의 클래스(Class)에 속할 확률을 추정합니다.

다중 분류는 소프트맥스 회귀(Softmax Regression)라고도 부르며, 소프트맥스 함수(Softmax Function)를 활용해 클래스에 포함될 확률을 계산합니다.

소프트맥스 함수(Softmax Function)

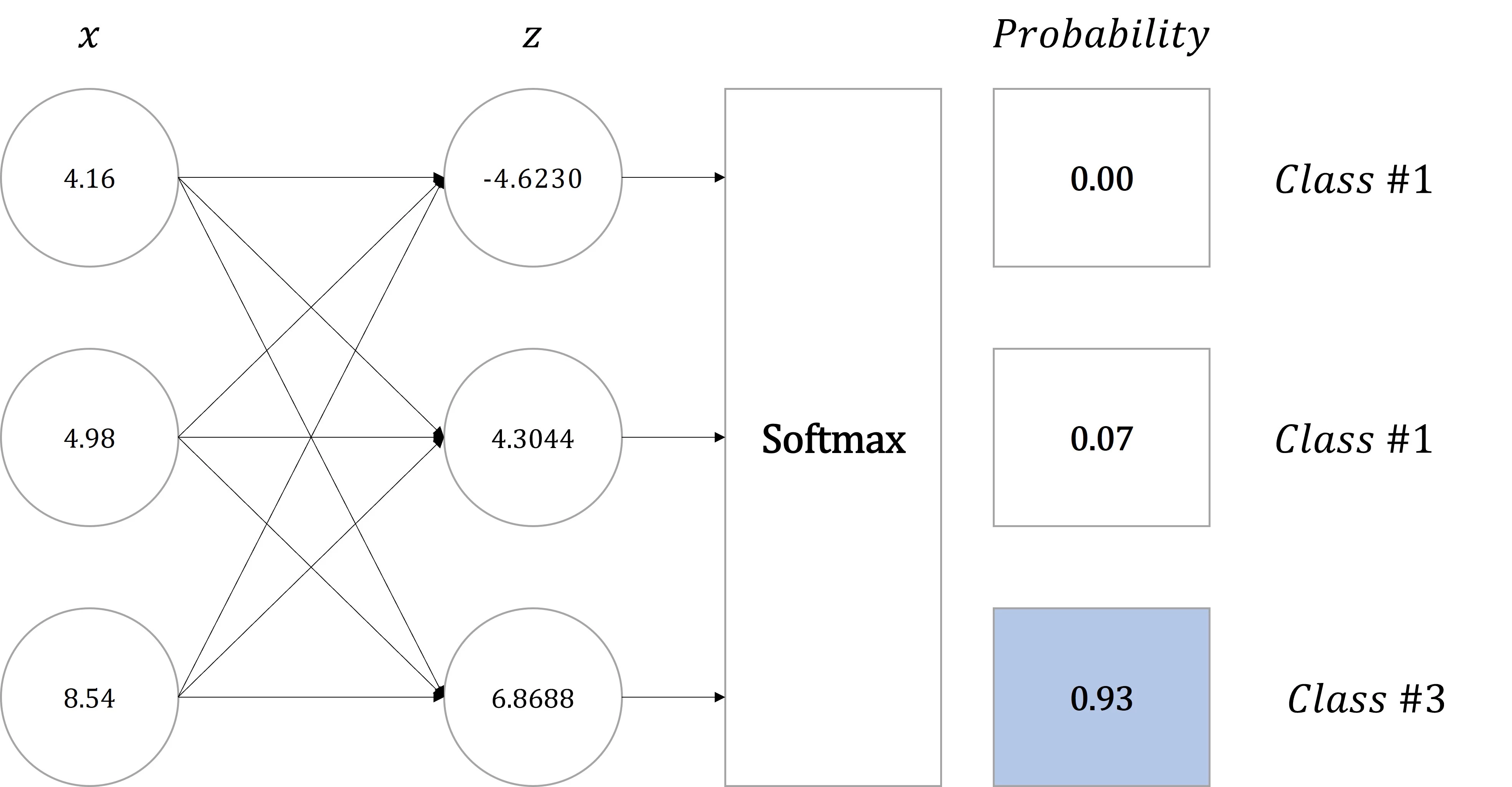
소프트맥스 함수(Softmax Function)는 출력층(Output Layer)을 통해 나온 예측값을 각각의 클래스에 속할 확률로 계산합니다.

만약 선형 변환(Linear Transformation, nn.Linear)의 구조로 생성된 모델에서 입력값이 $[4.16, 4.98, 8.54]$이며, 출력값이 $[-4.6230, 4.3044, 6.8688]$라면 세 번째(6.8688) 클래스에 포함되는 것은 알 수 있으나, 얼마나 높은 정확도로 세 번째(6.8688)에 클래스가 되는지 확인하기 어렵습니다.

또한, 두 번째(4.3044) 클래스 값과 세 번째(6.8688) 클래스의 차이가 얼마나 큰 영향을 미치는지 확인할 수 없습니다.

즉, 클래스를 결정한다고 가정했을 때 근소한 차이로 세 번째(6.8688)에 클래스가 되는지 높은 확률로 세 번째(6.8688) 클래스가 되는지 확인하기 어렵습니다.

그러므로 이 값을 확률의 형태로 변환하기 위해 소프트맥스 함수(Softmax Function)를 적용합니다.

소프트맥스 함수(Softmax Function)의 수식은 다음과 같습니다.

\[\begin{multline} \shoveleft p_{k} = \frac{e^{z_k}}{\sum_{i=1}^{n} e^{z_i} }\\ \shoveleft p_{n} = \frac{e^{z_n}}{e^{z_1}+e^{z_2}+e^{z_3}+...e^{z_n}}\\\\ \shoveleft softmax(z) = [p_{1}, p_{2}, p_{3}, ... p_{n}]\\ \end{multline}\]

소프트맥스 함수(Softmax Function)는 $n$ 차원 벡터에서 특정 출력 값이 $k$ 번째 클래스에 속할 확률을 계산합니다.

모든 $z$ 값의 합을 나누게 되므로 $p_1$ 부터 $p_n$ 까지의 합을 모두 더하면 1(=100%)이됩니다.

간략하게 설명한다면 출력값 $z$의 값의 합계가 1이 되도록 재조정하는 작업입니다.

위 그림에서 적용한 벡터값을 소프트맥스 함수(Softmax Function)를 적용하면 다음과 같습니다.

\[\begin{multline} \shoveleft p_{1} = \frac{e^{-4.6230}}{e^{-4.6230}+e^{4.3044}+e^{6.8688}} \simeq = 0.00\\ \shoveleft p_{2} = \frac{e^{4.3044}}{e^{-4.6230}+e^{4.3044}+e^{6.8688}} \simeq = 0.07\\ \shoveleft p_{3} = \frac{e^{6.8688}}{e^{-4.6230}+e^{4.3044}+e^{6.8688}} \simeq = 0.93\\\\ \shoveleft softmax(z) = [0.00, 0.07, 0.93]\\ \end{multline}\]

즉, 입력값 $[4.16, 4.98, 8.54]$는 93% 확률로 Class #3에 포함됩니다.

교차 엔트로피(Cross Entropy)

교차 엔트로피(Cross Entropy)는 분류해야하는 클래스가 3개 이상일 때 사용하는 비용 함수(Cost Function)입니다.

앞선 강좌에서 다룬 이진 교차 엔트로피(Binary Cross Entropy)와 유사한 방식으로 계산합니다.

교차 엔트로피(Cross Entropy)의 수식은 다음과 같습니다.

\[\begin{multline} \shoveleft CE = -\sum_{c=1}^{C}L_{c}logP_{c}\\ \end{multline}\]

$c$는 클래스를 의미하며, $C$는 클래스의 총 개수를 의미합니다. 클래스의 개수가 총 세 개라면, $C = 3$이 됩니다.

$P_{c}$는 소프트맥스 함수(Softmax Function)에서 다룬 각각의 클래스에 속할 확률을 의미합니다.

$L_{c}$는 실젯값의 원-핫 벡터(One-hot Vector)를 의미합니다.

원-핫 벡터(One-hot Vector)란 원-핫 인코딩(One-hot Encoding)을 통해 데이터가 벡터 형태로 변환된 형태를 의미합니다.

클래스의 개수와 동일한 길이를 가지면서, 각 클래스에 해당하는 색인값에 1을 부여하고 나머지 모든 값에 0을 부여합니다.

만약 클래스의 개수가 총 세 개이면서, 첫 번째 클래스에 해당하는 값을 표현하고 싶다면, 1이 아닌, $[1, 0, 0]$이 됩니다.

즉, Class #1, Class #2, Class #3가 있다면 각각 $[1, 0, 0]$, $[0, 1, 0]$, $[0, 0, 1]$으로 표현합니다.

앞선 예시를 통해서 교차 엔트로피(Cross Entropy)의 손실값을 계산한다면 다음과 같습니다.

입력값($X$) = $[4.16, 4.98, 8.54]$
출력값($\hat{Y}$) = $[-4.6230, 4.3044, 6.8688]$
실젯값($Y$) = $3$
- 세 번째 클래스를 의미합니다.
클래스의 총 개수($C$) = $3$
$L$ = $[0, 0, 1]$
- 실젯값이 3이며, 클래스의 총 개수가 3이므로, 원-핫 인코딩(One-hot Encoding)을 적용하면 $[0, 0, 1]$이 됩니다.
$P$ = $[0.00, 0.07, 0.93]$
- 소프트맥스 함수(Softmax Function) 적용 결과입니다.

$$ \begin{align} CE & = -\sum_{c=1}^{C}L_{c}logP_{c}\\\\ & = -\sum_{c=1}^{3}L_{c}logP_{c}\\\\ & = -(L_{1}logP_{1} + L_{2}logP_{2} + L_{3}logP_{3})\\\\ & = -(0log0.00 + 0log0.07 + 1log0.93)\\\\ & = -log0.93\\\\ & \simeq 0.03 \end{align} $$

교차 엔트로피(Cross Entropy)를 통해 입력값을 세 번째 클래스로 학습했을 때, 오차(Cost)를 계산한다면 $0.03$이 됩니다.

만약, 실젯값 세 번째 클래스가 아닌 두 번째 클래스였다면 다음과 같이 오차가 계산됩니다. ($L = [0, 1, 0]$)

$$ \begin{align} CE & = -(L_{1}logP_{1} + L_{2}logP_{2} + L_{3}logP_{3})\\\\ & = -(0log0.00 + 1log0.07 + 0log0.93)\\\\ & = -log0.07\\\\ & \simeq 1.15 \end{align} $$

실젯값과 출력값의 예측이 정확하다면 오차(Cost)는 0에 가까워지며, 정확하지 않을수록 오차는 0에서 멀어집니다.

학습은 교차 엔트로피(Cross Entropy)의 결과가 0에 가까워지는 방향으로 학습됩니다.

전체 데이터($n$개)를 대상으로 오차를 계산한다면, 수식은 다음과 같이 표현합니다.

\[CE = -\frac{1}{n}\sum_{i=1}^{n}\sum_{c=1}^{C}L_{c}logP_{c}\]

Tip : 클래스가 두 개라면, 이진 교차 엔트로피(Binary Cross Entropy)와 동일한 수식이 됩니다.

데이터 세트

학습에 사용된 dataset.csv는 아래 링크에서 다운로드할 수 있습니다.

Dataset 다운로드 : 다운로드

dataset.csv는 다음과 같은 형태로 구성되어 있습니다.

a	b	c	class
3.16	7.72	3.63	obtuse triangle
9.46	8.48	7.74	acute triangle
7.23	8.58	8.40	acute triangle
5.73	3.82	9.95	obtuse triangle
3.07	6.10	6.83	right triangle
…	…	…	…

a, b, c는 삼각형의 변의 길이를 의미하며, class는 어떤 삼각형인지 의미합니다.

클래스는 예각삼각형(acute triangle), 정삼각형(right triangle), 둔각삼각형(obtuse triangle)으로 구성되어 있습니다.

각 변의 길이는 원할한 학습을 위해 길이가 짧은 순으로 정렬되어 있습니다.

정삼각형(right triangle)은 각도가 90°에 근사한다면, 정삼각형으로 할당됐습니다.

이 데이터를 활용하여 다중 분류(Multiclass Classification)를 모델(Model)로 구현해보도록 하겠습니다.

메인 코드

import torch
import pandas as pd
from torch import nn
from torch import optim
from torch.utils.data import Dataset, DataLoader


class CustomDataset(Dataset):
    def __init__(self, file_path):
        df = pd.read_csv(file_path)
        self.a = df.iloc[:, 0].values
        self.b = df.iloc[:, 1].values
        self.c = df.iloc[:, 2].values
        self.y = df.iloc[:, 3].values
        self.y = list(map(self.string_to_vector, self.y))
        self.length = len(df)

    def string_to_vector(self, value):
        data = {"acute triangle": 0, "right triangle": 1, "obtuse triangle": 2}
        return data.get(value, None)

    def __getitem__(self, index):
        x = torch.FloatTensor(sorted([self.a[index], self.b[index], self.c[index]]))
        y = torch.LongTensor(self.y)[index]
        return x, y

    def __len__(self):
        return self.length


class CustomModel(nn.Module):
    def __init__(self):
        super(CustomModel, self).__init__()

        self.layer = nn.Sequential(
            nn.Linear(3, 3)
        )

    def forward(self, x):
        x = self.layer(x)
        return x


train_dataset = CustomDataset("./dataset.csv")
train_dataloader = DataLoader(train_dataset, batch_size=128, shuffle=True, drop_last=True)

device = "cuda" if torch.cuda.is_available() else "cpu"
model = CustomModel().to(device)
criterion = nn.CrossEntropyLoss().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.001)

for epoch in range(10000):
    cost = 0.0

    for x, y in train_dataloader:
        x = x.to(device)
        y = y.to(device)

        output = model(x)
        loss = criterion(output, y)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        cost += loss

    cost = cost / len(train_dataloader)

    if (epoch + 1) % 1000 == 0:
        print(f"Epoch : {epoch+1:4d}, Cost : {cost:.3f}")


with torch.no_grad():
    model.eval()
    classes = {0: "acute triangle", 1: "right triangle", 2: "obtuse triangle"}
    inputs = torch.FloatTensor([
        [9.02, 9.77, 9.96], # 0 | acute triangle
        [8.01, 8.08, 8.32], # 0 | acute triangle
        [3.55, 5.15, 6.26], # 1 | right triangle
        [3.32, 3.93, 5.14], # 1 | right triangle
        [4.39, 5.56, 9.99], # 2 | obtuse triangle
        [3.01, 3.08, 9.98], # 2 | obtuse triangle
        [5.21, 5.38, 5.39], # 0 | acute triangle
        [3.85, 6.23, 7.32], # 1 | right triangle
        [4.16, 4.98, 8.54], # 2 | obtuse triangle
    ]).to(device)
    outputs = model(inputs)
    
    print('---------')
    print(outputs)
    print(torch.round(F.softmax(outputs, dim=1), decimals=2))
    print(outputs.argmax(1))
    print(list(map(classes.get, outputs.argmax(1).tolist())))

결과: Epoch : 1000, Cost : 0.222
Epoch : 2000, Cost : 0.140
Epoch : 3000, Cost : 0.103
Epoch : 4000, Cost : 0.080
Epoch : 5000, Cost : 0.065
Epoch : 6000, Cost : 0.056
Epoch : 7000, Cost : 0.049
Epoch : 8000, Cost : 0.043
Epoch : 9000, Cost : 0.038
Epoch : 10000, Cost : 0.035
---------
tensor([[ 14.0070, 7.2270, -7.6265],
[ 12.6752, 6.1033, -7.0592],
[ 0.7832, 4.3076, 0.9737],
[ 0.9755, 3.4801, 0.6885],
[ -7.1158, 4.7455, 9.4825],
[-15.8092, 3.2274, 17.0585],
[ 8.2692, 4.3379, -4.9598],
[ 0.6708, 5.0402, 1.2550],
[ -4.6230, 4.3044, 6.8688]], device=’cuda:0’)
tensor([[1.0000, 0.0000, 0.0000],
[1.0000, 0.0000, 0.0000],
[0.0300, 0.9400, 0.0300],
[0.0700, 0.8700, 0.0500],
[0.0000, 0.0100, 0.9900],
[0.0000, 0.0000, 1.0000],
[0.9800, 0.0200, 0.0000],
[0.0100, 0.9700, 0.0200],
[0.0000, 0.0700, 0.9300]], device=’cuda:0’)
tensor([0, 0, 1, 1, 2, 2, 0, 1, 2], device=’cuda:0’)
[‘acute triangle’, ‘acute triangle’, ‘right triangle’, ‘right triangle’, ‘obtuse triangle’, ‘obtuse triangle’, ‘acute triangle’, ‘right triangle’, ‘obtuse triangle’]

세부 코드

class CustomDataset(Dataset):
    def __init__(self, file_path):
        df = pd.read_csv(file_path)
        self.a = df.iloc[:, 0].values
        self.b = df.iloc[:, 1].values
        self.c = df.iloc[:, 2].values
        self.y = df.iloc[:, 3].values
        self.y = list(map(self.string_to_vector, self.y))
        self.length = len(df)

    def string_to_vector(self, value):
        data = {"acute triangle": 0, "right triangle": 1, "obtuse triangle": 2}
        return data.get(value, None)

    def __getitem__(self, index):
        x = torch.FloatTensor(sorted([self.a[index], self.b[index], self.c[index]]))
        y = torch.LongTensor(self.y)[index]
        return x, y

    def __len__(self):
        return self.length

데이터 세트(Dataset) 클래스를 상속받아 사용자 정의 데이터 세트(CustomDataset)를 정의합니다.

초기화 메서드(__init__)에서 CSV 파일의 경로를 입력받을 수 있게 file_path를 정의합니다.

self.a, self.b, self.c에 a, b, c 값을 할당하며, self.y에 class 값을 할당합니다.

class 값은 문자열(string)로 구성되어 있으므로, string_to_vector 메서드로 각 클래스를 0, 1, 2의 값으로 변경합니다.

호출 메서드(__getitem__)에서 x는 입력값(x1, x2, x3)를 할당하고, y는 실젯값(y)를 반환합니다.

실젯값(y)는 0 ~ 2의 범위를 갖는 텐서이므로, 부호 있는 64 비트 정수(LongTensor)로 선언합니다.

criterion = nn.CrossEntropyLoss().to(device)

교차 엔트로피 클래스(nn.CrossEntropyLoss)로 criterion 인스턴스를 생성합니다.

교차 엔트로피 클래스(nn.CrossEntropyLoss)는 소프트맥스 함수(Softmax Function)와 원-핫 인코딩(One-hot Encoding)을 자체적으로 수행합니다.

즉, 학습에 적용되는 실젯값은 상수(0, 1, 2, …)로 입력합니다.

with torch.no_grad():
    model.eval()
    classes = {0: "acute triangle", 1: "right triangle", 2: "obtuse triangle"}
    inputs = torch.FloatTensor([
        [9.02, 9.77, 9.96], # 0 | acute triangle
        [8.01, 8.08, 8.32], # 0 | acute triangle
        [3.55, 5.15, 6.26], # 1 | right triangle
        [3.32, 3.93, 5.14], # 1 | right triangle
        [4.39, 5.56, 9.99], # 2 | obtuse triangle
        [3.01, 3.08, 9.98], # 2 | obtuse triangle
        [5.21, 5.38, 5.39], # 0 | acute triangle
        [3.85, 6.23, 7.32], # 1 | right triangle
        [4.16, 4.98, 8.54], # 2 | obtuse triangle
    ]).to(device)
    outputs = model(inputs)
    
    print('---------')
    print(outputs)
    print(torch.round(F.softmax(outputs, dim=1), decimals=2))
    print(outputs.argmax(1))
    print(list(map(classes.get, outputs.argmax(1).tolist())))

확률의 형태로 확인할수 있도록 출력값(outputs)에 소프트맥스 함수(F.softmax)를 적용합니다.

반올림 함수(torch.round)로 소숫점 두 번째 자리까지 표현합니다.

최댓값 색인위치(argmax) 함수로 출력값(outputs)에서 가장 높은 값을 지니는 값만 추출합니다.

맵(map) 함수로 해당 색인값에 맞는 삼각형 명칭으로 변경합니다.

출력 결과

# print(outputs)

tensor([[ 14.0070,   7.2270,  -7.6265],
        [ 12.6752,   6.1033,  -7.0592],
        [  0.7832,   4.3076,   0.9737],
        [  0.9755,   3.4801,   0.6885],
        [ -7.0864,   4.7449,   9.4535],
        [-15.8092,   3.2274,  17.0585],
        [  8.2692,   4.3379,  -4.9598],
        [  0.6708,   5.0402,   1.2550],
        [ -4.6230,   4.3044,   6.8688]], device='cuda:0')

출력값(outputs)을 통해 어떤 클래스로 계산되었는지 확인할 수 있습니다.

가장 높은 값을 지닌 색인 위치가 해당 클래스로 인식된 경우입니다.

[ 14.0070, 7.2270, -7.6265]는 14.0070가 가장 높은 값이므로, 예각삼각형(acute triangle)으로 예측되었다 볼 수 있습니다.

# print(torch.round(F.softmax(outputs, dim=1), decimals=2))

tensor([[1.0000, 0.0000, 0.0000],
        [1.0000, 0.0000, 0.0000],
        [0.0300, 0.9400, 0.0300],
        [0.0700, 0.8700, 0.0500],
        [0.0000, 0.0100, 0.9900],
        [0.0000, 0.0000, 1.0000],
        [0.9800, 0.0200, 0.0000],
        [0.0100, 0.9700, 0.0200],
        [0.0000, 0.0700, 0.9300]], device='cuda:0')

출력값(outputs)을 통해 어떤 클래스로 계산되었는지 확인할 수 있지만, 얼마나 높은 확률로 예측되었는지는 확인하기 어렵습니다.

소프트맥스 함수(F.softmax)를 적용하여 출력값의 예측 확률을 확인합니다.

# print(outputs.argmax(1))
# print(list(map(classes.get, outputs.argmax(1).tolist())))

tensor([0, 0, 1, 1, 2, 2, 0, 1, 2], device='cuda:0')
['acute triangle', 'acute triangle', 'right triangle', 'right triangle', 'obtuse triangle', 'obtuse triangle', 'acute triangle', 'right triangle', 'obtuse triangle']

출력값(outputs)을 다시 데이터 세트의 class에 표현된 방식과 동일한 형태로 변경합니다.

실젯값(inputs 주석)과 동일하게 반환된 것을 확인할 수 있습니다.

Kakao

Naver Twitter LinkedIn Facebook

Python Pytorch 강좌 : 제 13강 - 다중 분류(Multiclass Classification)

다중 분류(Multiclass Classification)

소프트맥스 함수(Softmax Function)

교차 엔트로피(Cross Entropy)

데이터 세트

메인 코드

세부 코드

출력 결과

공유하기

댓글 남기기

최근 포스트

Artificial Intelligence Theory : 가중치 초기화(Weight Initialization)

Artificial Intelligence Theory : 배치 정규화(Batch Normalization)

Artificial Intelligence Theory : 활성화 함수(Activation Function)