Python Pytorch 강좌 : 제 14강 - 퍼셉트론(Perceptron)
퍼셉트론(Perceptron)
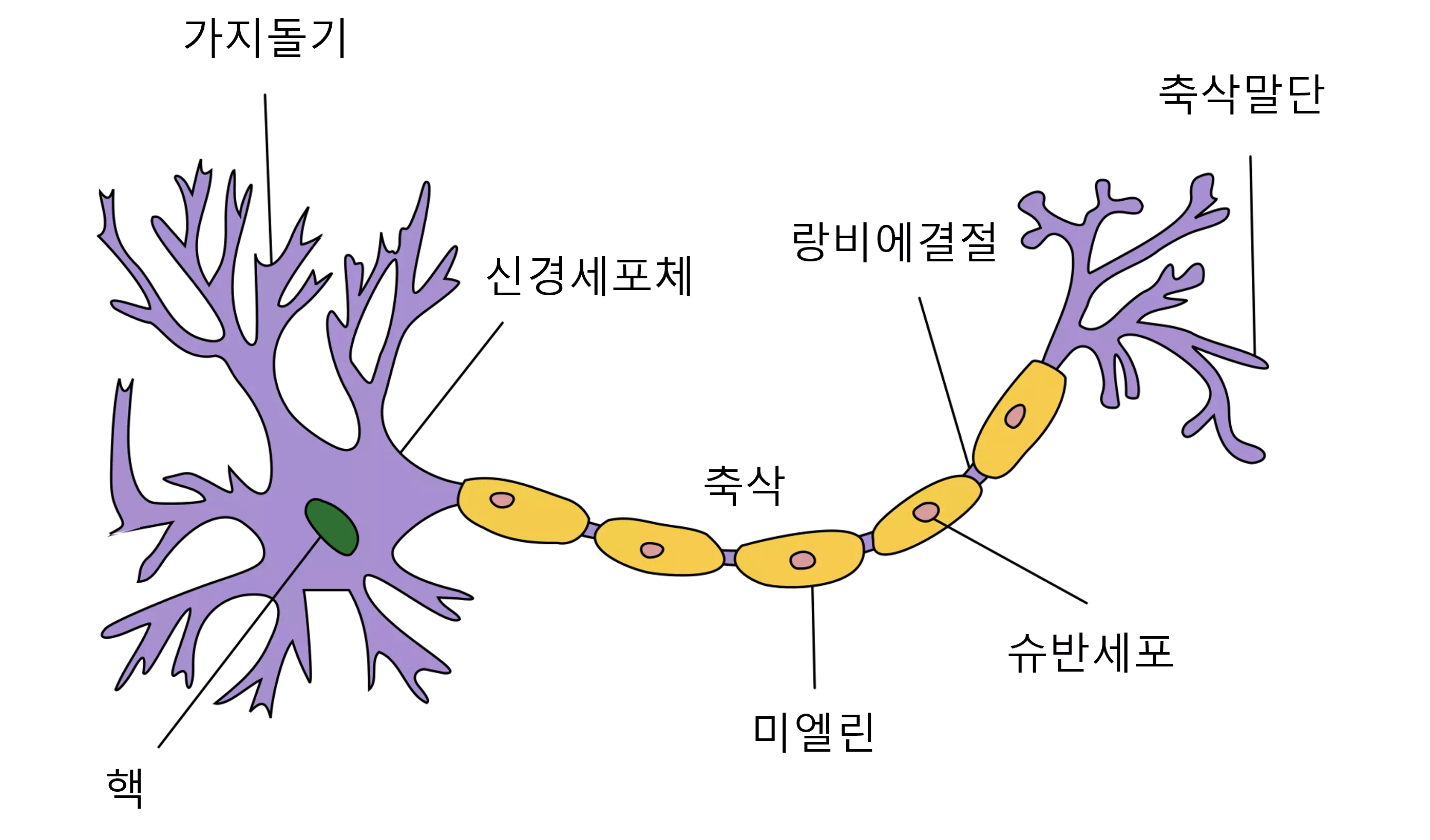
퍼셉트론(Perceptron)이란 인공 신경망의 한 종류로서, 코넬 항공 연구소(Cornell Aeronautical Lab)의 프랑크 로젠블라트(Frank Rosenblatt)에 의해 고안된 알고리즘입니다.
퍼셉트론(Perceptron)은 신경 세포(Neuron)가 신호를 전달하는 구조와 유사한 방식으로 구현됩니다.
생물학적 신경망에서는 가지돌기(Dendrite)가 외부의 신경 자극을 받아 신경세포체(Soma)에서 가중 압력을 받아 신호를 전달합니다.
전달되는 신호는 축삭(Axon)을 통해 다른 신경 세포(Neuron)로 최종 신호를 전달합니다.
신경 세포(Neuron)에서 다른 신경 세포(Neuron)로 신호를 전달할 때 시냅스(Synapse)라는 연결 부위를 통해 신호를 전달합니다.
이 때 전달되는 신호를 어느 정도의 세기로 전달할지 결정하게 됩니다. 퍼셉트론(Perceptron)은 이와 유사한 형태로 구성되어 있습니다.
가지돌기(Dendrite)는 입력값(X)을 전달 받는 역할을 합니다.
신경세포체(Soma)는 입력값(X)을 토대로 특정 연산을 진행했을 때 임곗값(Threshold)보다 크다면 전달하고, 작다면 전달하지 않습니다.
시냅스(Synapse)는 여러 퍼셉트론(Perceptron)을 연결한 형태가 됩니다.
퍼셉트론(Perceptron)은 TLU(Threshold Logic Unit) 형태를 기반으로 하며, 계단 함수(Step Function)를 적용해 결과를 반환합니다.
즉, 퍼셉트론(Perceptron)은 입력값(X)과 노드(Node)의 가중치(Weight)를 곱한 값을 모두 더했을때 임곗값(Threshold)`보다 크면 1을 출력하고, 작다면 0을 출력합니다.
그러므로 여러 입력값(\(x_{1}, x_{2}, x_{3} ... x_{n}\))을 입력했을 때, 0이나 1 또는 -1에서 1 사이의 값을 출력하는 모델을 의미합니다.
원본 이미지 출처 : Wikipedia
단층 퍼셉트론(Single Layer Perceptron)
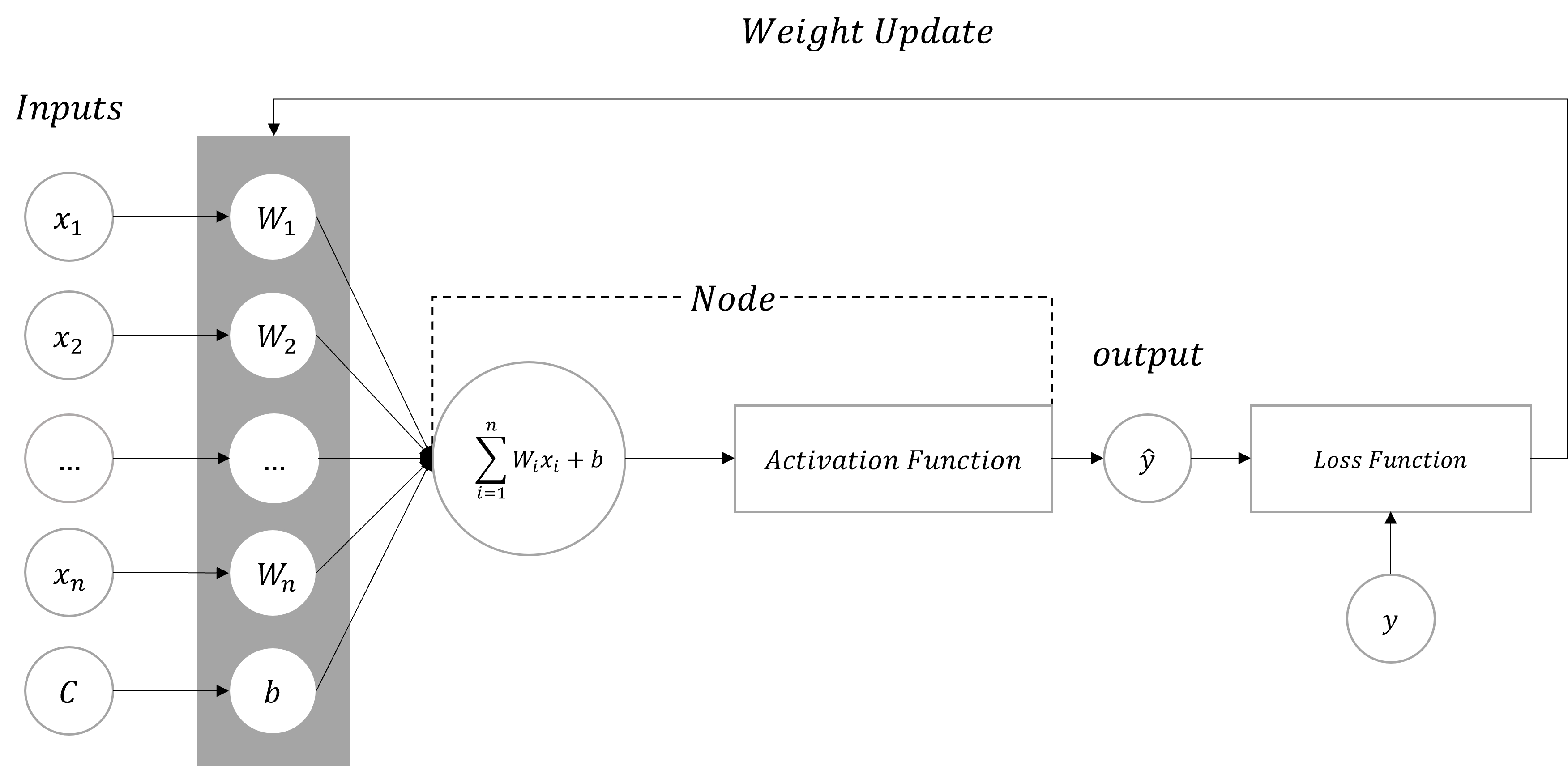
단층 퍼셉트론(Single Layer Perceptron)은 하나의 노드(Node)을 갖는 모델(Model)을 의미합니다.
입력(Inputs)을 통해 데이터가 전달되고 입력값(\(x\))은 각각의 가중치(Weight)와 함께 노드(Node)에 전달됩니다.
전달된 입력값(x)과 가중치(Weight)를 곱한 값이 활성화 함수(Activation Function)에 전달됩니다.
활성화 함수에서 출력값(\(\hat{y}\))이 계산되고 이 값을 손실 함수(Loss Function)에 실젯값(\(y\))과 함께 연산하여 가중치를 변경합니다.
단층 퍼셉트론(Single Layer Perceptron)은 앞선 강좌에서 다룬 모델 구조와 동일한 형태가 됩니다.
- Tip : 입력값
C는 \(1\)로b는 \(W_{0}\)으로 간주될 수 있습니다.
단층 퍼셉트론 한계
단층 퍼셉트론(Single Layer Perceptron)은 AND, OR, NAND 게이트와 같은 구조를 갖는 모델은 쉽게 구현할 수 있습니다.
하지만, XOR 게이트처럼 하나의 기울기로 표현하기 어려운 구조에서는 적용하기 어렵습니다.
위 그래프에서 XOR를 표현하려면 (0, 0) / (0, 1), (1, 0) / (1, 1)의 구조로 삼등분 되어야 합니다.
만약, (0, 0), (1, 1) / (0, 1), (1, 0)의 구조로 이등분하려 한다면 직선이 아닌 곡선의 형태가 되어 학습이 어려워질 뿐만 아니라, 과대적합(Overfitting) 문제도 발생합니다.
이러한 문제를 해결하기 위해 다층 퍼셉트론(Multi Layer Perceptron)를 활용합니다.
다층 퍼셉트론(Multi Layer Perceptron)
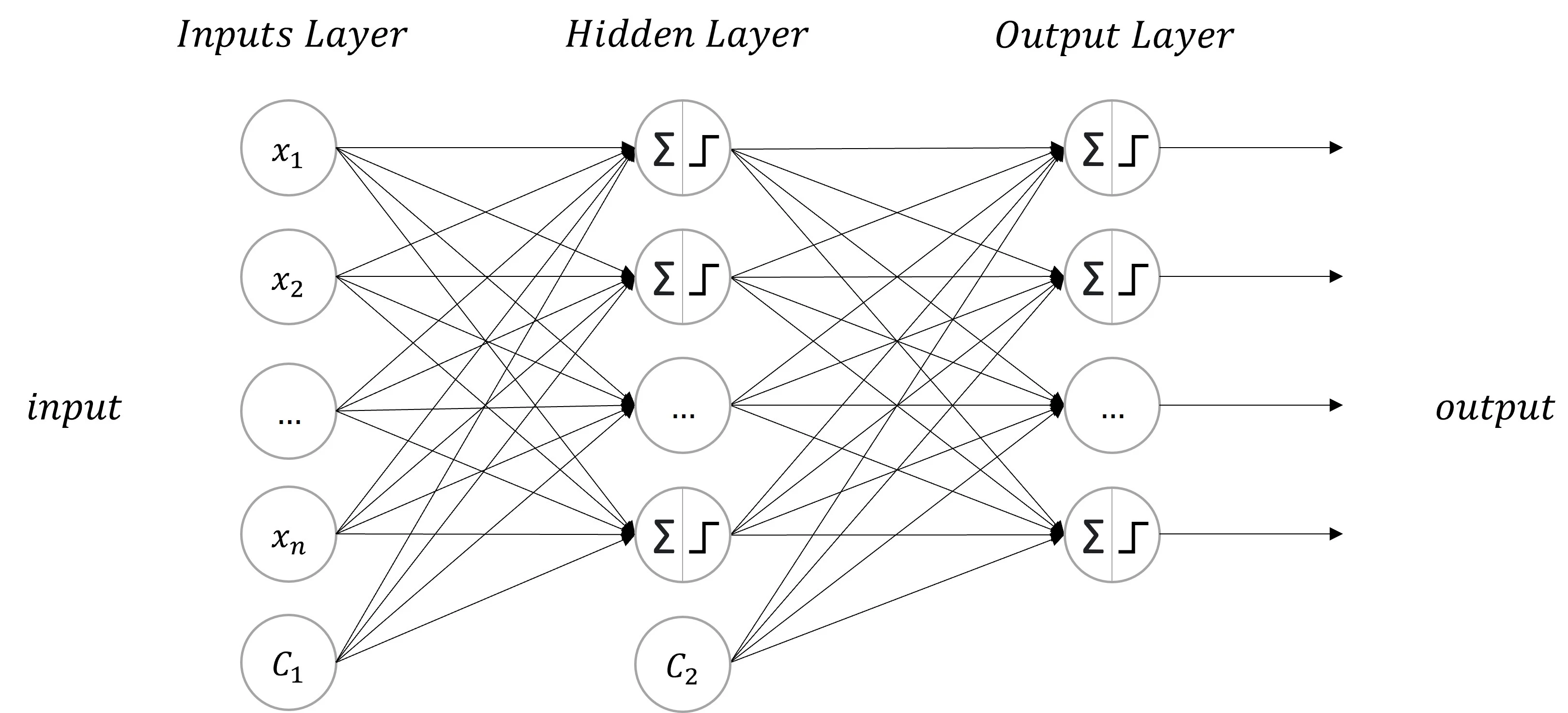
다층 퍼셉트론(Multi Layer Perceptron, MLP)은 단층 퍼셉트론(Single Layer Perceptron)을 여러 개 쌓아 은닉층(Hidden Layer)을 생성합니다.
다층 퍼셉트론은 은닉층(Hidden Layer)이 한 개 이상인 퍼셉트론 구조를 의미합니다.
은닉층(Hidden Layer)이 늘어나면 더 복잡한 구조의 문제를 해결할 수 있습니다.
은닉층이 2개 이상 연결하다면, 심층 신경망(Deep Neural Network, DNN)이라 부릅니다.
다층 퍼셉트론(Multi Layer Perceptron)은 학습 방법은 다음과 같습니다.
- 입력층부터 출력층까지
순전파(Forward Propagation)를 진행 - 출력값(예측값)과 실젯값으로
오차(Cost)계산 - 오차를 퍼셉트론의 역방향으로 보내면서, 입력된 뉴런의 기여도 측정
손실 함수(Loss Function)을 편미분해기울기(Gradient)계산연쇄 법칙(Chain Rule)을 통해 기울기를 계산
- 입력층에 도달할 때까지 뉴런의 기여도 측정
- 모든 가중치(Weight)에
최적화(Optimization)알고리즘 수행
즉, 역전파(Back Propagation) 과정을 통해 모든 노드의 가중치(Weight)를 수정하여 오차가 작아지는 방향으로 학습을 진행합니다.
순전파와 역전파에 대한 자세한 내용은 순전파(Forward Propagation) & 역전파(Back Propagation)에서 확인해볼 수 있습니다.
은닉층에 따른 문제 해결
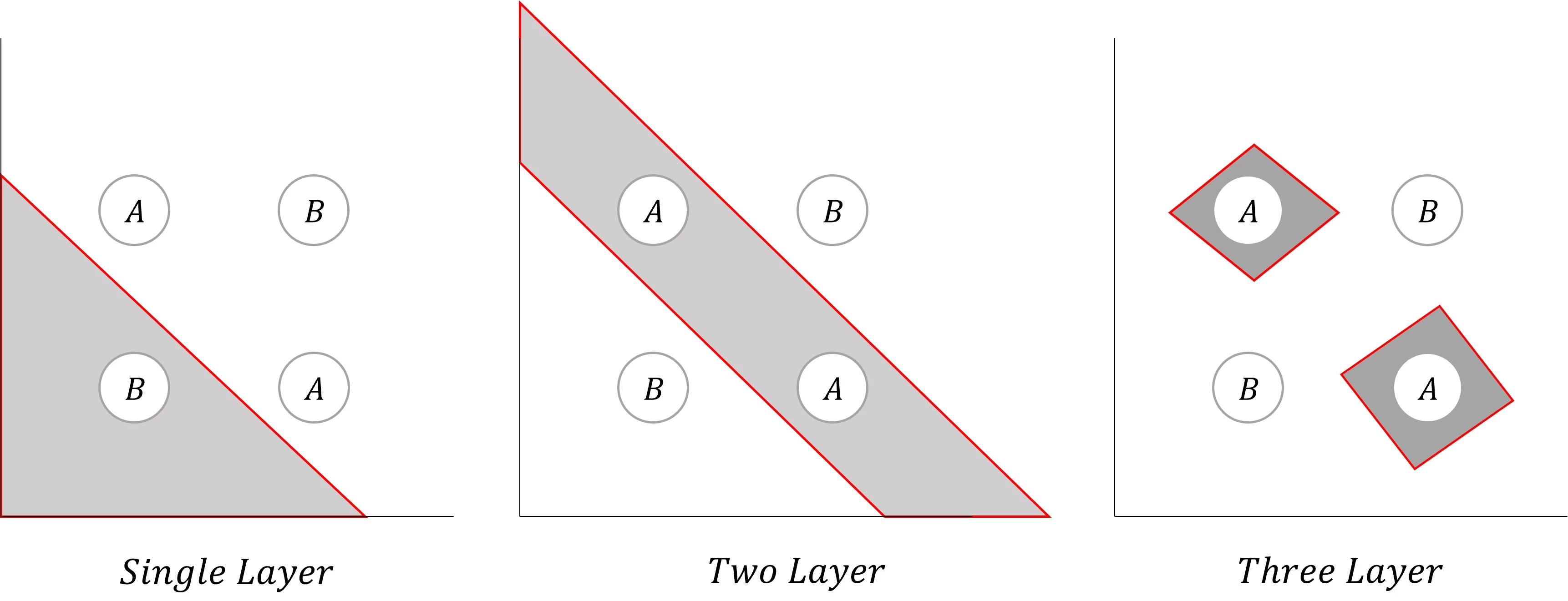
은닉층(Hidden Layer)의 수가 늘어날 수록 더 복잡한 문제를 해결할 수 있습니다.
하지만, 문제를 해결하기 위해 더 매개변수를 필요로 하게 되어 더 많은 학습 데이터를 요구하게 됩니다.
이는 모델 구현에 더 많은 데이터 수집 및 학습 시간을 필요로 하게 됩니다. 또한, 추론까지 걸리는 시간 및 비용이 증가합니다.
그러므로 해결하고자 하는 문제에 적합한 은닉층의 수로 모델을 구성해야 합니다.
- Tip :
은닉층(Hidden Layer)의 수가 많아지면 깊은(Deep) 모델이 됩니다.
데이터 세트
학습에 사용된 dataset.csv는 아래 링크에서 다운로드할 수 있습니다.
Dataset 다운로드: 다운로드
dataset.csv는 다음과 같은 형태로 구성되어 있습니다.
| x1 | x2 | y |
|---|---|---|
| True | True | False |
| True | False | True |
| True | False | True |
| False | True | True |
| False | False | False |
| … | … | … |
x1, x2는 입력값을 의미하며, y는 XOR 게이트를 통과했을 때의 결과를 의미합니다.
이 데이터를 활용하여 단층 퍼셉트론(Single Layer Perceptron)과 다층 퍼셉트론(Multi Layer Perceptron)을 적용한 모델(Model)로 구현해보도록 하겠습니다.
- Tip :
활성화 함수(Activation Function)를계단 함수(Step Function)로 적용하면 퍼셉트론(Perceptron)으로 부르며, 계단 함수가 아니라면인공 신경망(Neural Network)으로 부릅니다. - Tip : 현재 예제는
활성화 함수(Activation Function)에시그모이드(Sigmoid)를 적용해인공 신경망(Neural Network)입니다.
단층 퍼셉트론 모델
메인 코드
import torch
import pandas as pd
from torch import nn
from torch import optim
from torch.utils.data import Dataset, DataLoader
class CustomDataset(Dataset):
def __init__(self, file_path):
df = pd.read_csv(file_path)
self.x1 = df.iloc[:, 0].values
self.x2 = df.iloc[:, 1].values
self.y = df.iloc[:, 2].values
self.length = len(df)
def __getitem__(self, index):
x = torch.FloatTensor([self.x1[index], self.x2[index]])
y = torch.FloatTensor([self.y[index]])
return x, y
def __len__(self):
return self.length
class CustomModel(nn.Module):
def __init__(self):
super(CustomModel, self).__init__()
self.layer = nn.Sequential(
nn.Linear(2, 1),
nn.Sigmoid()
)
def forward(self, x):
x = self.layer(x)
return x
train_dataset = CustomDataset("./dataset.csv")
train_dataloader = DataLoader(train_dataset, batch_size=64, shuffle=True, drop_last=True)
device = "cuda" if torch.cuda.is_available() else "cpu"
model = CustomModel().to(device)
criterion = nn.BCELoss().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01)
for epoch in range(10000):
cost = 0.0
for x, y in train_dataloader:
x = x.to(device)
y = y.to(device)
output = model(x)
loss = criterion(output, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
cost += loss
cost = cost / len(train_dataloader)
if (epoch + 1) % 1000 == 0:
print(f"Epoch : {epoch+1:4d}, Cost : {cost:.3f}")
with torch.no_grad():
model.eval()
inputs = torch.FloatTensor([
[0, 0],
[0, 1],
[1, 0],
[1, 1]
]).to(device)
outputs = model(inputs)
print('---------')
print(outputs)
print(outputs <= 0.5)
결과
Epoch : 1000, Cost : 0.692
Epoch : 2000, Cost : 0.692
Epoch : 3000, Cost : 0.692
Epoch : 4000, Cost : 0.693
Epoch : 5000, Cost : 0.692
Epoch : 6000, Cost : 0.692
Epoch : 7000, Cost : 0.692
Epoch : 8000, Cost : 0.692
Epoch : 9000, Cost : 0.692
Epoch : 10000, Cost : 0.692
---------
tensor([[0.4675],
[0.4996],
[0.5041],
[0.5362]], device=’cuda:0’)
tensor([[ True],
[ True],
[False],
[False]], device=’cuda:0’)
단층 퍼셉트론(Single Layer Perceptron)으로 XOR 문제를 해결하려고 한다면, 비용(Cost)이 더 이상 감소되지 않는 것을 확인할 수 있습니다.
하나의 계층(Layer)으로는 XOR 게이트 문제를 해결할 수 없어서 발생하는 문제입니다.
모델에 값을 입력했을 때에도 출력값이 0.5 내외로 출력되어 학습이 정상적으로 진행되지 않은 것을 확인할 수 있습니다.
다층 퍼셉트론 모델
메인 코드
import torch
import pandas as pd
from torch import nn
from torch import optim
from torch.utils.data import Dataset, DataLoader
class CustomDataset(Dataset):
def __init__(self, file_path):
df = pd.read_csv(file_path)
self.x1 = df.iloc[:, 0].values
self.x2 = df.iloc[:, 1].values
self.y = df.iloc[:, 2].values
self.length = len(df)
def __getitem__(self, index):
x = torch.FloatTensor([self.x1[index], self.x2[index]])
y = torch.FloatTensor([self.y[index]])
return x, y
def __len__(self):
return self.length
class CustomModel(nn.Module):
def __init__(self):
super(CustomModel, self).__init__()
self.layer1 = nn.Sequential(
nn.Linear(2, 2),
nn.Sigmoid()
)
self.layer2 = nn.Sequential(
nn.Linear(2, 1),
nn.Sigmoid()
)
def forward(self, x):
x = self.layer1(x)
x = self.layer2(x)
return x
train_dataset = CustomDataset("./dataset.csv")
train_dataloader = DataLoader(train_dataset, batch_size=64, shuffle=True, drop_last=True)
device = "cuda" if torch.cuda.is_available() else "cpu"
model = CustomModel().to(device)
criterion = nn.BCELoss().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01)
for epoch in range(10000):
cost = 0.0
for x, y in train_dataloader:
x = x.to(device)
y = y.to(device)
output = model(x)
loss = criterion(output, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
cost += loss
cost = cost / len(train_dataloader)
if (epoch + 1) % 1000 == 0:
print(f"Epoch : {epoch+1:4d}, Cost : {cost:.3f}")
with torch.no_grad():
model.eval()
inputs = torch.FloatTensor([
[0, 0],
[0, 1],
[1, 0],
[1, 1]
]).to(device)
outputs = model(inputs)
print('---------')
print(outputs)
print(outputs <= 0.5)
결과
Epoch : 1000, Cost : 0.693
Epoch : 2000, Cost : 0.691
Epoch : 3000, Cost : 0.631
Epoch : 4000, Cost : 0.433
Epoch : 5000, Cost : 0.108
Epoch : 6000, Cost : 0.045
Epoch : 7000, Cost : 0.027
Epoch : 8000, Cost : 0.019
Epoch : 9000, Cost : 0.015
Epoch : 10000, Cost : 0.012
---------
tensor([[0.0134],
[0.9890],
[0.9890],
[0.0130]], device=’cuda:0’)
tensor([[ True],
[False],
[False],
[ True]], device=’cuda:0’)
다층 퍼셉트론(Multi Layer Perceptron)의 구조로 계층(Layer)을 두 개 사용하여 모델을 학습합니다.
학습이 진행될 수록 비용(Cost)이 감소하는 것을 확인할 수 있습니다.
또한, 모델에 값을 입력했을 때에도 출력값이 0에 가까워지거나, 1에 가까워지는 것을 확인할 수 있으므로 학습이 정상적으로 진행된 것을 확인할 수 있습니다.
공유하기
 Kakao
Kakao
 Naver
Twitter
LinkedIn
Facebook
Naver
Twitter
LinkedIn
Facebook
댓글 남기기