Python Pytorch 강좌 : 제 4강 - 손실 함수(Loss Function)

손실 함수(Loss Function)

손실 함수(Loss Function)는 실젯값과 예측값이 차이가 발생했을 때 오차가 얼마인지 계산하는 함수입니다.

인공 신경망(Neural Network)은 실젯값과 예측값을 통해 계산된 오찻값을 최소화 시켜 정확도를 높이는 방법으로 학습이 진행됩니다.

그러므로, 각 데이터의 오차를 계산하게 되는데 이 때 사용되는 함수를 손실 함수(Loss Function)라고 합니다.

손실 함수는 목적 함수(Objective Function), 비용 함수(Cost Function)라고 부르기도 합니다.

목적 함수(Objective Function)는 함숫값의 결과를 최댓값 또는 최솟값으로 최적화 시키는 함수이며, 비용 함수(Cost Function)는 전체 데이터에 대한 오차를 계산하는 함수입니다.

즉, 목적 함수(Objective Function) → 비용 함수(Cost Function) → 손실 함수(Loss Function)의 형태로 포함된다 볼 수 있습니다.

손실 함수(Loss Function), 목적 함수(Objective Function), 비용 함수(Cost Function)는 모두 오차를 최소화시키기 위해 사용되기 때문에 동일한 의미로 사용되기도 합니다.

하지만, 의미를 정확히 구분해 사용하는 것이 좋습니다.

다음 표와 그래프는 앞선 제 3강 - 가설(Hypothesis)의 데이터에서 선형 회귀 그래프에 대한 예측값과 실젯값의 오차를 포함합니다.

X	Y(실젯값)	예측값	오차
1	0.94	0.443	0.497
2	1.98	1.322	0.658
3	2.88	2.201	0.679
4	3.92	3.08	0.84
5	3.96	3.959	0.001
6	4.55	4.838	-0.288
7	5.64	5.717	-0.077
8	6.3	6.596	-0.296
9	7.44	7.475	-0.035
10	9.1	8.354	0.746
…	…	…	…

$$ \begin{multline} \shoveleft H(x) = Wx + b\\ \shoveleft W = 0.879\\ \shoveleft b = -0.436\\\\ \shoveleft \therefore \ H(x) = 0.879x - 0.436 \end{multline} $$

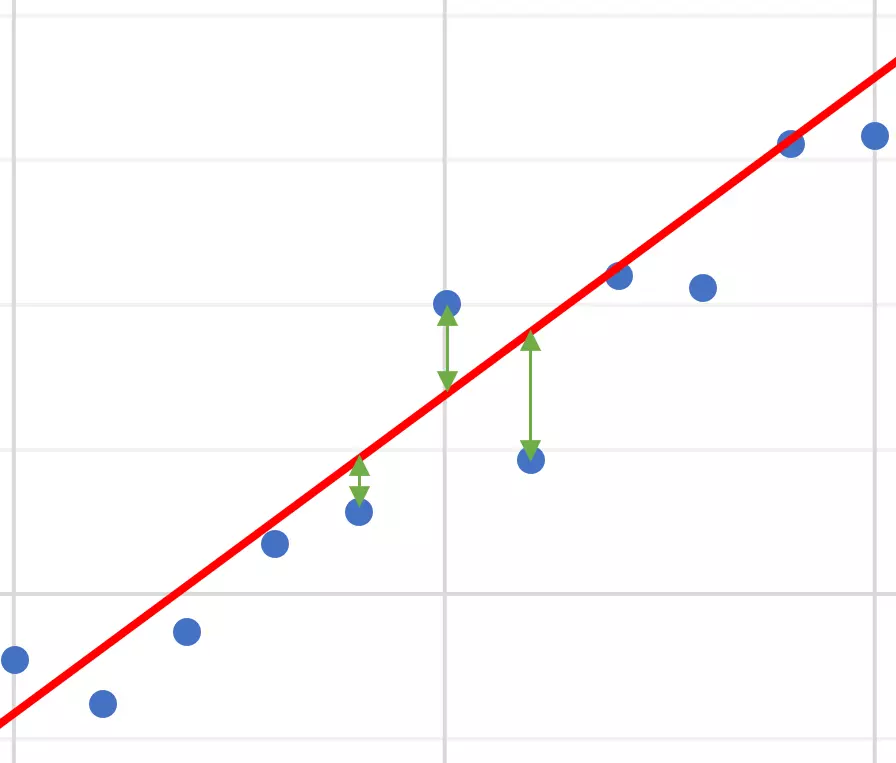
위 표의 오차는 모집단(Population)에서 실젯값 - 예측값에 대한 수치입니다.

우측 그래프에서 오차는 녹색 화살표로 표현하였습니다.

오차는 예측값이 얼마나 실젯값을 잘 표현하는지 알 수 있습니다.

하지만, 이러한 방법은 각각의 데이터에 대한 오차를 확인할 수 있는 방법이므로 가설(Hypothesis)이 얼마나 실젯값을 정확하게 표현하는지는 알 수 없습니다.

그러므로, 평균 제곱 오차(Mean Squared Error, MSE)을 활용하여 생성된 가설이 얼마나 정확하게 표현하는지 계산합니다.

• Tip : 만약, 표본집단(Sample)에서 실젯값 - 예측값에 대한 수치를 계산하였다면 오차(Error)가 아닌, 잔차(Residual)라 부릅니다.

제곱 오차(Squared Error, SE)

위 수식에서 사용된 평균 제곱 오차(Mean Squared Error, MSE) 방법은 제곱 오차(Squared Error, SE)와 오차 제곱합(Sum of Squared for Error, SSE)를 활용합니다.

먼저 제곱 오차(Squared Error)는 실젯값과 예측값을 감산한 값의 제곱을 의미합니다.

수식으로 표현한다면 다음과 같습니다.

만약, 제곱을 취하지 않는다면 양의 방향이나 음의 방향의 오차의 차이를 알 수 있지만 방향보다는 오차의 크기가 중요한 요소기 때문에 제곱을 취하게 됩니다.

제곱 대신에 절댓값을 취하지 않는 이유로는 제곱을 적용하면 비교적 오차가 작은 값보다 오차가 큰 값을 확대시키기 때문에 오차의 간극을 빠르게 확인할 수 있습니다.

즉, 제곱을 취하기 때문에 오차가 커질수록 각 데이터마다 오차의 크기를 빠르게 확인할 수 있습니다.

오차 제곱합(Sum of Squared for Error, SSE)

오차 제곱합(Sum of Squared for Error)은 제곱 오차(Squared Error)를 모두 더한 값이 됩니다.

제곱 오차(Squared Error)는 각 데이터마다의 오차를 의미하므로 가설(Hypothesis) 또는 모델(Model) 자체가 얼마나 정확히 예측을 하는지 알 수 없습니다.

그러므로, 모든 제곱 오차를 더하여 하나의 값으로 가설이나 모델을 평가할 수 있습니다.

수식으로 표현한다면 다음과 같습니다.

만약 여기서도 오찻값들을 제곱하지 않고 모두 더하는 방법이라면 문제가 발생하게됩니다.

오찻값이 (-1, 1, -1, 1)과 같은 형태라면 모든 합계가 0이 되어 오차가 없는 것처럼 보여집니다.

이러한 현상을 방지하기 위해 모든 값을 제곱한 값에 대한 평균으로 오차를 계산합니다.

평균 제곱 오차(Mean Squared Error, MSE)

평균 제곱 오차(Mean Squared Error, MSE) 방법은 단순하게 오차 제곱합(Sum of Squared for Error, SSE)에서 평균을 취하는 방법입니다.

오차 제곱합과 평균 제곱 오차는 의미로는 큰 차이가 없지만, 데이터가 많아질수록 오차 제곱합도 동일하게 커지게 됩니다.

이렇게 되는 경우 오차가 많은 것인지 데이터가 많은 것인지 구분하기가 어려워지므로, 모든 데이터의 개수만큼 나누어 평균을 취합니다.

평균 제곱 오차 방법을 수식으로 표현하고 위 데이터의 값을 적용한다면 다음과 같습니다.

평균 제곱 오차는 가설의 품질을 측정할 수 있으며, 오차가 0에 가까워질수록 높은 품질을 갖게 됩니다.

주로 회귀 분석(Regression)에서 많이 사용되는 손실 함수이며, 최대 신호 대 잡음비(Peak Signal-to-noise ratio, PSNR)를 계산하는데에도 사용됩니다.

또한, 이 값에 루트(Root)를 씌우는 경우에는 평균 제곱근 오차(Root Mean Squared Error, RMSE)가 됩니다.

루트를 통해 평균 제곱 오차(Mean Squared Error, MSE)에서 발생한 왜곡을 감소시켜, 정밀도(Precision)를 표현하는데 적합한 형태가 됩니다.

• Tip : 오차에 제곱을 적용하여 오차량이 큰 값을 크게 부풀렸기 때문에 왜곡이 발생합니다.