Python Pytorch 강좌 : 제 3강 - 가설(Hypothesis)
가설(Hypothesis)
가설(Hypothesis)이란 어떤 사실을 설명하거나 증명하기 위한 가정으로 두 개 이상의 변수의 관계를 검증 가능한 형태로 기술하여 변수 간의 관계를 예측하는 것을 의미합니다.
가설에는 크게 연구 가설(Research Hypothesis), 귀무 가설(Null Hypothesis)과 대립 가설(Alternative Hypothesis)로 나눌 수 있습니다.
연구 가설(Research Hypothesis)은 연구자가 검증하려는 가설로 귀무 가설을 부정하는 것으로 설정한 가설을 증명하려는 가설입니다.
귀무 가설(Null Hypothesis)은 통계학에서 처음부터 버릴 것을 예상하는 가설입니다. 변수 간 차이나 관계가 없음을 통계학적 증거를 통해 증명하려는 가설입니다.
대립 가설(Alternative Hypothesis)은 귀무 가설과 반대되는 가설로 귀무 가설이 거짓이라면 대안으로 참이되는 가설입니다.
즉, 대립 가설은 연구 가설과 동일하다고 볼 수 있습니다. 이를 통해 통계적 가설 검정(Statistical Hypothesis Test)을 진행할 수 있습니다.
예를 들어, 나의 출근 시간이 평균적으로 오전 9시라는 가설을 가정한다면 귀무 가설과 대립 가설은 다음과 같이 표현될 수 있습니다.
- 귀무 가설 : \(\mu = 9\)
- 대립 가설 (1) : \(\mu \neq 9\)
- 대립 가설 (2) : \(\mu < 9\)
- 대립 가설 (3) : \(\mu > 9\)
기계 학습에서의 가설
기계 학습(Machine Learning)에서의 가설은 통계적 가설 검정(Statistical Hypothesis Test)이 되며, 데이터간에 변수 간의 관계가 있는지 확률론적으로 설명하게 됩니다.
즉, 기계 학습에서의 가설은 독립 변수(X)와 종속 변수(Y)를 가장 잘 매핑(Mapping)시키는 기능을 학습하기 위해 사용합니다.
그러므로 독립 변수와 종속 변수간에 관계를 가장 잘 근사(Approximation)시키기 위해 사용됩니다.
단일 가설(Single Hypothesis)은 \(h\)로 나타내고, 가설 집합(Hypothesis Set)은 \(H\)로 나타냅니다.
단일 가설(Single Hypothesis)은 입력을 출력에 매핑하고 평가하고 예측하는 데 사용할 수 있는 단일 모델(Model)을 의미합니다.
가설 집합(Hypothesis Set)은 출력에 입력을 매핑하기 위한 가설 공간(Hypothesis Space)으로 모든 가설을 의미합니다.
가설 표현
| X | Y |
|---|---|
| 1 | 0.91 |
| 2 | 1.84 |
| 3 | 2.91 |
| 4 | 3.64 |
| 5 | 4.6 |
| 6 | 6 |
| 7 | 6.51 |
| 8 | 6.72 |
| 9 | 8.46 |
| 10 | 10 |
| … | … |
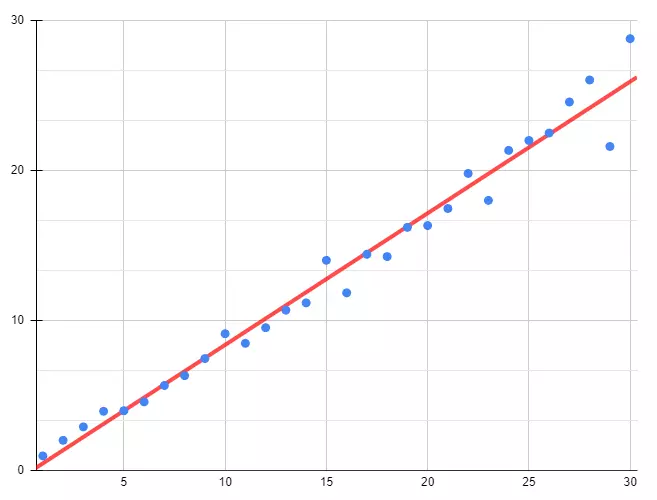
만약 독립 변수(X)와 종속 변수(Y)의 관계가 다음과 같다고 가정했을 때, 데이터와 그래프를 보여줍니다.
데이터(X, Y)를 기반으로 가설(Hypothesis)을 세울 수 있게 됩니다.
빨간색 선이 가설(Hypothesis)을 의미하며, 선형 회귀(Linear Regression)를 통해 계산된 값입니다.
수식으로는 \(y = ax + b\)로 표현할 수 있습니다.
\(a\) 는 기울기가 되며, \(b\)는 절편이 됩니다. 단, 기계 학습에서는 \(y = ax + b\)의 형태가 아닌 \(H(x) = Wx + b\)로 표현합니다.
\(H(x)\)는 가설(Hypothesis), \(W\)는 가중치(Weight), \(b\)는 편향(Bias)을 의미합니다.
기계 학습에서는 회귀 분석(Regression)을 통해 최적의 가중치(Weight)와 편향(Bias)을 찾는 과정을 진행하게 됩니다.
학습이 진행될 때 마다 기울기와 편향이 지속적으로 바뀌게 됩니다.
마지막으로 학습이 된 결과를 모델(Model)이라 부르며, 이 모델을 통해 새로운 입력값을 예측(prediction)하게 됩니다.
공유하기
 Kakao
Kakao
 Naver
Twitter
LinkedIn
Facebook
Naver
Twitter
LinkedIn
Facebook
댓글 남기기