Python OpenCV 강좌 : 제 25강 - 모멘트
모멘트(Moments)

윤곽선(contour)이나 이미지(array)의 0차 모멘트부터 3차 모멘트까지 계산하는 알고리즘입니다.
공간 모멘트(spatial moments), 중심 모멘트(central moments), 정규화된 중심 모멘트(normalized central moments), 질량 중심(mass center) 등을 계산할 수 있습니다.
메인 코드
import cv2
src = cv2.imread("Image/convex.png")
dst = src.copy()
gray = cv2.cvtColor(src, cv2.COLOR_RGB2GRAY)
ret, binary = cv2.threshold(gray, 150, 255, cv2.THRESH_BINARY_INV)
contours, hierarchy = cv2.findContours(binary, cv2.RETR_CCOMP, cv2.CHAIN_APPROX_NONE)
for i in contours:
M = cv2.moments(i)
cX = int(M['m10'] / M['m00'])
cY = int(M['m01'] / M['m00'])
cv2.circle(dst, (cX, cY), 3, (255, 0, 0), -1)
cv2.drawContours(dst, [i], 0, (0, 0, 255), 2)
cv2.imshow("dst", dst)
cv2.waitKey(0)
cv2.destroyAllWindows()세부 코드
for i in contours:
M = cv2.moments(i, False)
cX = int(M['m10'] / M['m00'])
cY = int(M['m01'] / M['m00'])cv2.moments()를 활용해 윤곽선에서 모멘트를 계산합니다.
cv2.moments(배열, 이진화 이미지)을 의미합니다.
배열은 윤곽선 검출 함수에서 반환되는 구조 또는 이미지를 사용합니다.
이진화 이미지는 입력된 배열 매개변수가 이미지일 경우, 이미지의 픽셀 값들을 이진화 처리할지 결정합니다.
이진화 이미지 매개변수에 참 값을 할당한다면 이미지의 픽셀 값이 0이 아닌 값은 모두 1의 값으로 변경해 모멘트를 계산합니다.
모멘트 함수를 통해 면적, 평균, 분산 등을 간단하게 구할 수 있습니다.
중심점을 구하는 공식은 다음과 같습니다.
위의 공식을 활용해 무게 중심(중심점)을 계산할 수 있습니다.
추가 정보
공간 모멘트(spatial moments)
\[m_{ij} = \sum_{x,y}(array(x,y)\times x^{i}y^{i})\]중심 모멘트(central moments)
\[mu_{ij} = \sum_{x,y}(array(x,y)\times (x-\bar{x})^{i}(y-\bar{y})^{j})\]정규화된 중심 모멘트(normalized central moments)
\[nu_{ij} = {mu_{ij}\over m_{00}^{ \frac{i+j}{2}+1} }\]모멘트 구조
\[\text{M} = \begin{cases} \text{0차 모멘트:}&m_{00}\\ \text{1차 모멘트:}&m_{10}, m_{01}\\ \text{2차 모멘트:}&m_{11}, m_{20}, m_{02}\\ \text{3차 모멘트:}&mu_{11}, mu_{20}, mu_{02}\\ \text{2차 중심 모멘트:}&mu_{11}, mu_{20}, mu_{02}\\ \text{3차 중심 모멘트:}&mu_{21}, mu_{12}, mu_{30}, mu_{03}\\ \text{2차 정규화된 중심 모멘트:}&nu_{11}, nu_{20}, nu_{02}\\ \text{3차 정규화된 중심 모멘트:}&nu_{21}, nu_{12}, nu_{30}, nu_{03}\\ \end{cases}\]반환되지 않는 값
\[\begin{cases} mu_{00} = m_{00}\\ nu_{00} = 1\\ mu_{01} = mu_{10} = nu_{01} = nu_{10} = 0 \end{cases}\]- Tip : 위 값들은 항상 같은 값을 가짐으로써 반환하지 않습니다.
출력 결과
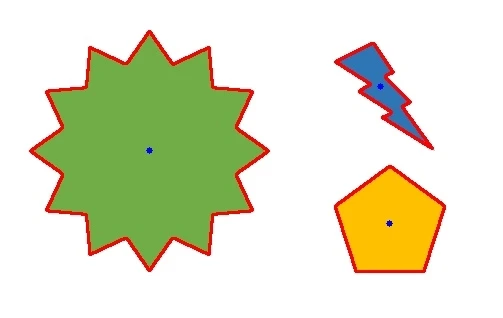
공유하기
 Kakao
Kakao
 Naver
Twitter
LinkedIn
Facebook
Naver
Twitter
LinkedIn
Facebook
댓글 남기기