상위 목록: 하위 목록: 작성 날짜: 읽는 데 34 분 소요

직선 검출(Line Detection)

직선 검출 알고리즘은 허프 변환(Hough Transform)을 활용해 직선을 검출합니다.

허프 변환은 이미지에서 직선을 찾는 가장 보편적인 알고리즘입니다.

이미지에서 선과 같은 단순한 형태를 빠르게 검출할 수 있으며, 직선을 찾아 이미지나 영상을 보정하거나 복원합니다.

허프 선 변환은 이미지 내의 어떤 점이라도 선 집합의 일부일 수 있다는 가정하에 직선의 방정식을 이용해 직선을 검출한다.

직선 검출은 직선의 방정식을 활용해 \(y = ax + b\)를 극좌표(ρ, θ)의 점으로 변환해서 사용합니다.

극좌표 방정식으로 변환한다면 \(p = xsinθ + ycosθ\)이 되어, 직선과 원점의 거리(ρ)와 직선과 x축이 이루는 각도(θ)를 구할 수 있습니다.



표준 허프 변환(Standard Hough Transform) & 멀티 스케일 허프 변환(Multi-Scale Hough Transform)

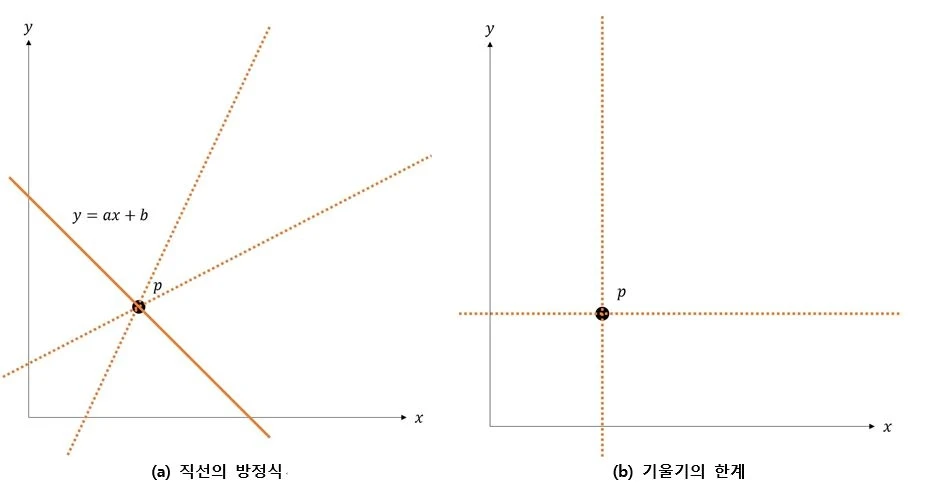
표준 허프 변환(Standard Hough Transform)은 입력 이미지(x, y 평면) 내의 점 \(p\)를 지나는 직선의 방정식을 구합니다.

한 점을 통과하는 직선의 방정식을 구하면 기울기 \(a\)와 절편 \(b\)를 구할 수 있습니다.

점 \(p\)에 대해 직선의 방정식을 수식으로 표현하면 그림 (a)와 같이 \(y = ax + b\) 로 표현할 수 있습니다.

모든 점에 대해 모든 직선의 방정식을 구한다면 평면상에서 점들의 궤적이 생성되며, 동일한 궤적 위의 점은 직선으로 볼 수 있습니다.

하지만, 한 점을 지나는 모든 직선의 방정식을 표현한다면 그림 (b)와 같이 기울기 \(a\)는 음의 무한대(-∞)에서 양의 무한대(∞)의 범위를 갖습니다.

또한 수평인 영역에서 기울기 \(a\) 는 \(0\)의 값을 갖습니다.

기울기와 절편을 사용해 모든 직선의 방정식을 표현하는 것은 좋은 방식이 아니므로, 삼각함수를 활용해 각 선을 극좌표(ρ, θ)의 점으로 변환해서 나타냅니다.


멀티 스케일 허프 변환(Multi-Scale Hough Transform)은 표준 허프 변환을 개선한 방법입니다.

검출한 직선의 값이 더 정확한 값으로 반환되도록, 거리(ρ)와 각도(θ)의 값을 조정해 사용합니다.

두 값을 조정하는 방법으로 조금 더 우수한 검출을 할 수 있습니다.



메인 코드

import numpy as np
import cv2

src = cv2.imread("road.jpg")
dst = src.copy()
gray = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)
canny = cv2.Canny(gray, 5000, 1500, apertureSize = 5, L2gradient = True)
lines = cv2.HoughLines(canny, 0.8, np.pi / 180, 150, srn = 100, stn = 200, min_theta = 0, max_theta = np.pi)

for i in lines:
    rho, theta = i[0][0], i[0][1]
    a, b = np.cos(theta), np.sin(theta)
    x0, y0 = a*rho, b*rho

    scale = src.shape[0] + src.shape[1]

    x1 = int(x0 + scale * -b)
    y1 = int(y0 + scale * a)
    x2 = int(x0 - scale * -b)
    y2 = int(y0 - scale * a)

    cv2.line(dst, (x1, y1), (x2, y2), (0, 0, 255), 2)
    cv2.circle(dst, (x0, y0), 3, (255, 0, 0), 5, cv2.FILLED)

cv2.imshow("dst", dst)
cv2.waitKey(0)
cv2.destroyAllWindows()


세부 코드

src = cv2.imread("road.jpg")
dst = src.copy()
gray = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)
canny = cv2.Canny(gray, 5000, 1500, apertureSize = 5, L2gradient = True)

이미지에서 직선을 검출하기 위해서, 전처리 작업을 진행합니다.

원본 이미지(src)와 결과 이미지(dst)를 선언합니다.

전처리를 진행하기 위해 그레이스케일 이미지(gray)와 케니 엣지 이미지(canny)를 사용합니다.

케니 엣지 알고리즘의 임곗값은 각각 5000과 1500로 주요한 가장자리만 남깁니다.

커널은 5의 크기와 L2그라디언트를 True로 사용합니다.


lines = cv2.HoughLines(canny, 0.8, np.pi / 180, 150, srn = 100, stn = 200, min_theta = 0, max_theta = np.pi)

cv2.HoughLines(검출 이미지, 거리, 각도, 임곗값, 거리 약수, 각도 약수, 최소 각도, 최대 각도)를 이용하여 직선 검출을 진행합니다.

거리와 각도는 누산 평면에서 사용되는 해상도를 나타냅니다.

거리의 단위는 픽셀을 의미하며, 0.0 ~ 1.0의 실수 범위를 갖습니다.

각도의 단위는 라디안을 사용하며 0 ~ 180의 범위를 갖습니다.

임곗값은 허프 변환 알고리즘이 직선을 결정하기 위해 만족해야 하는 누산 평면의 값을 의미합니다.

누산 평면은 각도 × 거리의 차원을 갖는 2차원 히스토그램으로 구성됩니다.

거리 약수와 각도 약수는 거리와 각도에 대한 약수(divisor)를 의미합니다.

두 값 모두 0의 값을 인수로 활용할 경우, 표준 허프 변환이 적용되며, 하나 이상의 값이 0이 아니라면 멀티 스케일 허프 변환이 적용됩니다.

최소 각도와 최대 각도는 검출할 각도의 범위를 설정합니다.


for i in lines:
    rho, theta = i[0][0], i[0][1]
    a, b = np.cos(theta), np.sin(theta)
    x0, y0 = a*rho, b*rho

    scale = src.shape[0] + src.shape[1]

    x1 = int(x0 + scale * -b)
    y1 = int(y0 + scale * a)
    x2 = int(x0 - scale * -b)
    y2 = int(y0 - scale * a)

    cv2.line(dst, (x1, y1), (x2, y2), (0, 0, 255), 2)
    cv2.circle(dst, (x0, y0), 3, (255, 0, 0), 5, cv2.FILLED)

검출을 통해 반환되는 lines 변수는 (N, 1, 2)차원 형태를 갖습니다.

내부 차원의 요소로는 검출된 거리(rho)와 각도(theta)가 저장돼 있습니다.

반복문을 활용해 lines 배열에서 거리와 각도를 반환할 수 있으며, 거리와 각도를 다시 직선의 방정식의 형태로 구성해야 결과 이미지 위에 표현할 수 있습니다.

x와 y는 각각 \(x = rcosθ\), \(r = sinθ\)의 형태를 가지므로, 이 수식을 활용해 \(x0\)와 \(y0\)의 좌표를 구합니다.

허프 변환 함수는 시작점과 도착점을 알려주는 함수가 아닌, 가장 직선일 가능성이 높은 거리와 각도를 검출합니다.

검출된 정보는 직선의 방정식에 더 가깝습니다. 그러므로 출력 이미지 위에 표현하기 위해 \(x0\)와 \(y0\)를 직선의 방정식 선분을 따라 평행이동시켜 선을 그립니다.

scale에 적절한 값을 지정해 이미지 밖으로 \(x1, y1, x2, y2\)를 할당합니다.

선 그리기 함수와 원 그리기 함수를 활용해 (x1, y1) ~ (x2, y2)와 (x0, y0)의 위치를 표시합니다.



점진성 확률적 허프 변환(Progressive Probabilistic Hough Transform)

점진성 확률적 허프 변환(Progressive Probabilistic Hough Transform)은 또 다른 허프 변환 함수를 사용해 직선을 검출합니다.

앞선 알고리즘은 모든 점에 대해 직선의 방정식을 세워 계산하기 때문에 비교적 많은 시간이 소모됩니다.

기본적으로 점진성 확률적 허프 변환 알고리즘은 앞선 알고리즘을 최적화한 방식입니다.

모든 점을 대상으로 직선의 방정식을 세우는 것이 아닌, 임의의 점 일부만 누적해서 계산합니다.

일부의 점만 사용하기 때문에 확률적입니다.

그러므로, 정확도가 높은 입력 이미지에 대해 검출에 드는 시간이 대폭 줄어듭니다.

또한 이 알고리즘은 시작점과 끝점을 반환하므로 더 간편하게 활용할 수 있습니다.



메인 코드

import numpy as np
import cv2

src = cv2.imread("road.jpg")
dst = src.copy()
gray = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)
canny = cv2.Canny(gray, 5000, 1500, apertureSize = 5, L2gradient = True)
lines = cv2.HoughLinesP(canny, 0.8, np.pi / 180, 90, minLineLength = 10, maxLineGap = 100)

for i in lines:
    cv2.line(dst, (int(i[0][0]), int(i[0][1])), (int(i[0][2]), int(i[0][3])), (0, 0, 255), 2)

cv2.imshow("dst", dst)
cv2.waitKey(0)
cv2.destroyAllWindows()


세부 코드

lines = cv2.HoughLinesP(canny, 0.8, np.pi / 180, 90, minLineLength = 10, maxLineGap = 100)

cv2.HoughLinesP(검출 이미지, 거리, 각도, 임곗값, 최소 선 길이, 최대 선 간격)를 이용하여 직선 검출을 진행합니다.

검출 이미지, 거리, 각도, 임곗값은 앞선 허프 변환 알고리즘 함수와 동일한 의미를 갖습니다.

최소 선 길이는 검출된 직선이 가져야 하는 최소한의 선 길이를 의미합니다. 이 값보다 낮은 경우 직선으로 간주하지 않습니다.

최대 선 간격은 검출된 직선들 사이의 최대 허용 간격을 의미합니다. 이 값보다 간격이 좁은 경우 직선으로 간주하지 않습니다.


for i in lines:
    cv2.line(dst, (int(i[0][0]), int(i[0][1])), (int(i[0][2]), int(i[0][3])), (0, 0, 255), 2)

검출을 통해 반환되는 lines 변수는 (N, 1, 4)차원 형태를 갖습니다.

마지막 차원에서 x1, y1, x2, y2의 순서로 시작점과 끝점을 표시합니다.

별도의 계산 없이 선 그리기 함수를 활용해 (x1, y1) ~ (x2, y2)의 위치를 표시합니다.



출력 결과

멀티 스케일 허프 변환(Multi-Scale Hough Transform)


점진성 확률적 허프 변환(Progressive Probabilistic Hough Transform)

댓글 남기기

최근 포스트